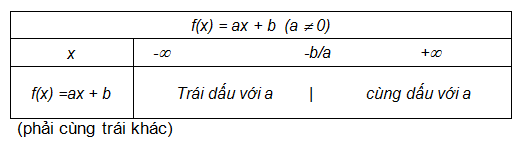Bài 2 trang 94 SGK Đại số 10
Giải các bất phương trình...
Video hướng dẫn giải
Giải các bất phương trình
a) \(\frac{2}{x-1}\leq \frac{5}{2x-1};\)
b) \(\frac{1}{x+1}<\frac{1}{(x-1)^{2}};\)
c) \(\frac{1}{x}+\frac{2}{x+4}<\frac{3}{x+3};\)
d) \(\frac{x^{2}-3x+1}{x^{2}-1}<1.\)
LG a
\(\dfrac{2}{x-1}\leq \dfrac{5}{2x-1};\)
Phương pháp giải:
- Biến đổi bất phương trình về dạng: f(x) > 0 hoặc f(x) < 0.
- Xét dấu của biểu thức f(x), để biết biểu thức f(x) nhận giá trị dương, âm với những giá trị nào của x.
Bảng xét dấu của nhị thức bậc nhất được thể hiện qua bảng sau:
Lời giải chi tiết:
\(\dfrac{2}{x-1}\leq \dfrac{5}{2x-1}\)
\( \Leftrightarrow \dfrac{2}{{x - 1}} - \dfrac{5}{{2x - 1}} \le 0\) \( \Leftrightarrow \dfrac{{2\left( {2x - 1} \right) - 5\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {2x - 1} \right)}} \le 0\) \( \Leftrightarrow \dfrac{{4x - 2 - 5x + 5}}{{\left( {x - 1} \right)\left( {2x - 1} \right)}} \le 0\) \( \Leftrightarrow \dfrac{{ - x + 3}}{{\left( {x - 1} \right)\left( {2x - 1} \right)}} \le 0\)
Xét \(f\left( x \right) = \dfrac{{ - x + 3}}{{\left( {x - 1} \right)\left( {2x - 1} \right)}}\)
Ta có:
\(\begin{array}{l}
- x + 3 = 0 \Leftrightarrow x = 3\\
2x - 1 = 0 \Leftrightarrow x = \dfrac{1}{2}\\
x - 1 = 0 \Leftrightarrow x = 1\\
\left( {\dfrac{1}{2} < 1 < 3} \right)
\end{array}\)
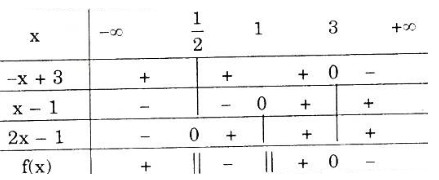
Tập nghiệm của bất phương trình là \(T = \left ( \dfrac{1}{2};1 \right ) ∪ [3; +∞)\).
LG b
\(\dfrac{1}{x+1}<\dfrac{1}{(x-1)^{2}};\)
Lời giải chi tiết:
\(\begin{array}{l}
\Leftrightarrow \dfrac{1}{{x + 1}} - \dfrac{1}{{{{\left( {x - 1} \right)}^2}}} < 0\\
\Leftrightarrow \dfrac{{{{\left( {x - 1} \right)}^2} - \left( {x + 1} \right)}}{{\left( {x + 1} \right){{\left( {x - 1} \right)}^2}}} < 0\\
\Leftrightarrow \dfrac{{{x^2} - 2x + 1 - x - 1}}{{\left( {x + 1} \right){{\left( {x - 1} \right)}^2}}} < 0\\
\Leftrightarrow \dfrac{{{x^2} - 3x}}{{\left( {x + 1} \right){{\left( {x - 1} \right)}^2}}} < 0\\
\Leftrightarrow \dfrac{{x\left( {x - 3} \right)}}{{\left( {x + 1} \right){{\left( {x - 1} \right)}^2}}} < 0
\end{array}\)
Xét \(f\left( x \right) = \dfrac{{x\left( {x - 3} \right)}}{{\left( {x + 1} \right){{\left( {x - 1} \right)}^2}}}\)
Ta có:
\(\begin{array}{l}
x = 0\\
x - 3 = 0 \Leftrightarrow x = 3\\
x + 1 = 0 \Leftrightarrow x = - 1\\
{\left( {x - 1} \right)^2} = 0 \Leftrightarrow x = 1\\
\left( { - 1 < 0 < 1 < 3} \right)
\end{array}\)
Xét dấu của \(f(x)\) ta được bảng xét dấu:
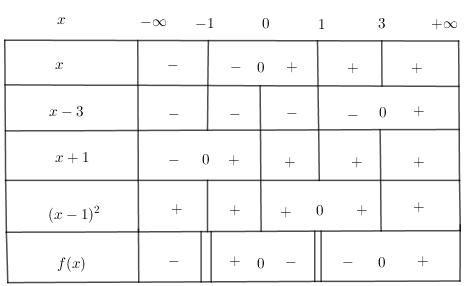
Tập nghiệm của bất phương trình là: \(T = (-∞; - 1) ∪ (0; 1) ∪ (1; 3)\).
LG c
\(\dfrac{1}{x}+\dfrac{2}{x+4}<\dfrac{3}{x+3};\)
Lời giải chi tiết:
\(\begin{array}{l}\dfrac{1}{x} + \dfrac{2}{{x + 4}} < \dfrac{3}{{x + 3}}\\ \Leftrightarrow \dfrac{1}{x} + \dfrac{2}{{x + 4}} - \dfrac{3}{{x + 3}} < 0\end{array}\)
\( \Leftrightarrow \dfrac{{\left( {x + 4} \right)\left( {x + 3} \right)}}{{x\left( {x + 4} \right)\left( {x + 3} \right)}} + \dfrac{{2x\left( {x + 3} \right)}}{{x\left( {x + 4} \right)\left( {x + 3} \right)}}\) \( - \dfrac{{3x\left( {x + 4} \right)}}{{x\left( {x + 4} \right)\left( {x + 3} \right)}} < 0\)
\( \Leftrightarrow \dfrac{{\left( {x + 4} \right)\left( {x + 3} \right) + 2x\left( {x + 3} \right) - 3x\left( {x + 4} \right)}}{{x\left( {x + 3} \right)\left( {x + 4} \right)}} < 0\)
\( \Leftrightarrow \dfrac{{{x^2} + 7x + 12 + 2{x^2} + 6x - 3{x^2} - 12x}}{{x\left( {x + 3} \right)\left( {x + 4} \right)}} < 0\)
\( \Leftrightarrow \dfrac{{x + 12}}{{x\left( {x + 3} \right)\left( {x + 4} \right)}} < 0\)
Xét \(f\left( x \right) = \dfrac{{x + 12}}{{x\left( {x + 3} \right)\left( {x + 4} \right)}}\)
Bảng xét dấu:
Ta có:
\(\begin{array}{l}
x = 0\\
x + 12 = 0 \Leftrightarrow x = - 12\\
x + 4 = 0 \Leftrightarrow x = - 4\\
x + 3 = 0 \Leftrightarrow x = - 3
\end{array}\)
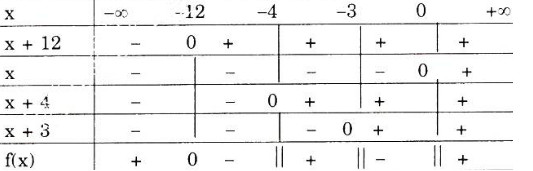
Tập nghiệm của bất phương trình là: \(T = \left ( -12;-4 \right ) ∪ (-3; 0)\).
LG d
\(\dfrac{x^{2}-3x+1}{x^{2}-1}<1.\)
Lời giải chi tiết:
\(\begin{array}{l}
\dfrac{{{x^2} - 3x + 1}}{{{x^2} - 1}} < 1\\
\Leftrightarrow \dfrac{{{x^2} - 3x + 1}}{{{x^2} - 1}} - 1 < 0\\
\Leftrightarrow \dfrac{{{x^2} - 3x + 1 - {x^2} + 1}}{{{x^2} - 1}} < 0\\
\Leftrightarrow \dfrac{{ - 3x + 2}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0
\end{array}\)
Xét \(f\left( x \right) = \dfrac{{ - 3x + 2}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)
Ta có:
\(\begin{array}{l}
- 3x + 2 = 0 \Leftrightarrow x = \dfrac{2}{3}\\
x + 1 = 0 \Leftrightarrow x = - 1\\
x - 1 = 0 \Leftrightarrow x = 1
\end{array}\)
Bảng xét dấu:
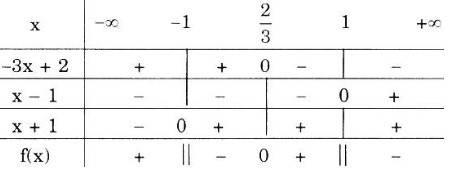
Tập nghiệm của bất phương trình là: \(T = \left ( -1;\dfrac{2}{3} \right ) ∪ (1; +∞)\).
Loigiaihay.com
- Bài 3 trang 94 SGK Đại số 10
- Bài 1 trang 94 SGK Đại số 10
- Câu hỏi 4 trang 92 SGK Đại số 10
- Câu hỏi 3 trang 92 SGK Đại số 10
- Câu hỏi 2 trang 90 SGK Đại số 10
>> Xem thêm