 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Ôn tập cuối năm - Hình học - Toán 8
Ôn tập cuối năm - Hình học - Toán 8
Bài 2 trang 131 SGK Toán 8 tập 2
Cho hình thang ABCD (AB // CD) có hai đường chéo cắt nhau ở O và tam giác ABO là tam giác đều.
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Đề bài
Cho hình thang \(ABCD \;(AB // CD)\) có hai đường chéo cắt nhau ở \(O\) và tam giác \(ABO\) là tam giác đều. Gọi \(E, F, G\) theo thứ tự là trung điểm của các đoạn thẳng \(OA, OD\) và \(BC\). Chứng minh rằng tam giác \(EFG\) là tam giác đều.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Dấu hiệu nhận biết tam giác đều.
- Tính chất đường trung bình của tam giác.
- Tính chất tamm giác đều.
Lời giải chi tiết
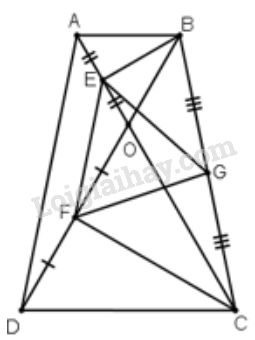
Vì tam giác \(ABO\) đều (giả thiết)
\( \Rightarrow \widehat {AOB} = \widehat {OAB} = \widehat {ABO} = {60^0}\) (tính chất tam giác đều)
Vì \(AB // CD\) (gt)
\( \Rightarrow \left\{ \begin{array}{l}
\widehat {O{\rm{D}}C} = \widehat {ABO} = {60^0}\left( {so\,le\,trong} \right)\\
\widehat {OC{\rm{D}}} = \widehat {OAB} = {60^0}\left( {so\,le\,trong} \right)
\end{array} \right.\)
Mà \(\widehat {CO{\rm{D}}} = \widehat {AOB} = {60^0}\) (đối đỉnh)
\( \Rightarrow\) tam giác \(CDO\) cũng đều (dấu hiệu nhận biết tam giác đều)
\( \Rightarrow OD = OC\) (tính chất tam giác đều)
Xét \(∆AOD\) và \(∆BOC\) có:
+) \(AO = BO\) (tam giác \(ABO\) đều)
+) \(\widehat {AO{\rm{D}}} = \widehat {BOC}\) (đối đỉnh)
+) \(OD = OC\) (cmt)
\( \Rightarrow ∆AOD = ∆BOC\) (c.g.c)
\( \Rightarrow AD = BC\) (2 cạnh tương ứng)
Ta có: \(E, F\) là trung điểm của \(AO\) và \(DO\) (gt)
\( \Rightarrow\) \(EF\) là đường trung bình của tam giác \(AOD\) (dấu hiệu nhận biết đường trung bình của tam giác)
\(EF = \dfrac{1}{2}AD = \dfrac{1}{2}BC\) (1) (tính chất đường trung bình của tam giác)
\(CF\) là đường trung tuyến của tam giác đều \(CDO\) nên \(CF ⊥ DO\) (tính chất tam giác đều)
Trong tam giác vuông \(CFB\), \(FG\) là đường trung tuyến ứng với cạnh huyền nên:
\(FG = \dfrac{1}{2}BC\) (2)
Chứng minh tương tự:
\(BE\) là đường trung tuyến của tam giác đều \(ABO\) nên \(BE ⊥ AO\) (tính chất tam giác đều)
Trong tam giác vuông \(CEB\), \(EG\) là đường trung tuyến ứng với cạnh huyền nên:
\(EG = \dfrac{1}{2}BC\) (3)
Từ (1), (2), (3) suy ra \(EF = GF = EG\) nên tam giác \(EFG\) là tam giác đều (dấu hiệu nhận biết tam giác đều)
Loigiaihay.com
- Bài 3 trang 131 SGK Toán 8 tập 2
- Bài 4 trang 132 SGK Toán 8 tập 2
- Bài 5 trang 132 SGK Toán 8 tập 2
- Bài 6 trang 132 SGK Toán 8 tập 2
- Bài 7 trang 132 SGK Toán 8 tập 2
>> Xem thêm











