Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học

Bài tập ôn tập chương 3

Bài 59 trang 102 SGK Đại số 10 nâng cao

Biện luận số nghiệm của mỗi phương trình bằng đồ thị.

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

Cho các phương trình:

$x^2+ 3x - m + 1 = 0$ (1) và $2x^2- x + 1 - 2p = 0$ (2)

a) Biện luận số nghiệm của mỗi phương trình bằng đồ thị.

b) Kiểm tra lại kết quả trên bằng phép tính.

LG a

Biện luận số nghiệm của mỗi phương trình bằng đồ thị.

Lời giải chi tiết:

* Xét phương trình ${x^2} + {\rm{ }}3x{\rm{ }}-{\rm{ }}m{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0$

Ta có: (1) $\Leftrightarrow {\rm{ }}{x^2} + {\rm{ }}3x{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}m{\rm{ }}$

Gọi (d) là đường thẳng $y = m$ .

Đồ thị hàm số $y = x^2+ 3x + 1$ là parabol (P) có đỉnh là điểm $(-1,5; -1,25)$ và hướng bề lõm lên trên.

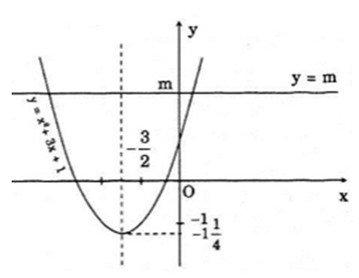
Do đó:

+ Khi $m < -1, 25$ thì (d) không cắt (P), phương trình vô nghiệm.

+ Khi $m = -1,25$ thì (d) và (P) có một điểm chung, phương trình có một nghiệm.

+ Khi $m > -1,25$ thì (d) cắt (P) tại hai điểm. Phương trình có hai nghiệm phân biệt.

* Xét phương trình $2x^2- x + 1 – 2p = 0$ (2)

(2) $⇔ 2x^2 – x + 1 = 2p$

Gọi (d) là đường thẳng $y = 2p$ ; (P) là parabol $y = 2x^2– x + 1$

Parabol (P) có đỉnh tại điểm: $({1 \over 4};\,{7 \over 8})$ và hướng bề lõm lên trên.

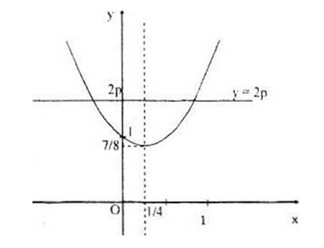
Do đó:

+ Nếu $2p < {7 \over 8}$ , tức là $p < {7 \over {16}}$ thì (d) không cắt (P), phương trình vô nghiệm.

+ Nếu $2p = {7 \over 8}$ , tức là $p = {7 \over {16}}$ thì (d) và (P) có một điểm chung, phương trình có một nghiệm.

+ Nếu $2p > {7 \over 8}$ , tức là $p > {7 \over {16}}$ thì (d) cắt (P) tại hai điểm chung, phương trình có hai nghiệm.

LG b

Kiểm tra lại kết quả trên bằng phép tính.

Lời giải chi tiết:

Xét phương trình (1) có : ${\Delta _1}$ = 9 + 4m – 4 = 4m + 5

- Nếu 4m + 5 < 0 ⇔ m < -5/4 = -11/4 thì (1) vô nghiệm

- Nếu 4m + 5 = 0 ⇔ m = -11/4 thì (1) có nghiệm kép

- Nếu 4m + 5 > 0 ⇔ m > -11/4 thì (1) có hai nghiệm phân biệt

Rõ ràng kết quả biện luận bằng đồ thị số nghiệm của (1) và kết quả biện luận số nghiệm của (1) bằng phép tính là như nhau.

Xét phương trình :

2x² – x + 1 – 2p = 0, có ${\Delta _2}$ = 1 – 8 + 16p = 16p - 7

- Nếu 16p – 7 < 0 ⇔ p < 7/16 thì (2) vô nghiệm

- Nếu 16p – 7 = 0 ⇔ p = 7/16 thì (2) có nghiệm kép x = 1/4

- Nếu 16p – 7 > 0 ⇔ p > 7/16 thì (2) có hai nghiệm phân biệt

Ta thấy kết quả biện luận số nghiệm bằng đồ thị và kết quả biện luận số nghiệm của (2) bằng phép tính là như nhau.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4 trên 6 phiếu

Bài tiếp theo

Bài 60 trang 102 SGK Đại số 10 nâng cao
Giải các hệ phương trình
Bài 61 trang 102 SGK Đại số 10 nâng cao
Giải và biện luận các hệ phương trình
Bài 62 trang 102 SGK Đại số 10 nâng cao
Giải và biện luận các hệ phương trình
Bài 63 trang 102 SGK Đại số 10 nâng cao
Tìm a, b và c để Parabol y = ax2 + bx + c có đỉnh là 1(1; -4) và đi qua điểm M(2; -3). Hãy vẽ Parabol nhận được.
Bài 64 trang 102 SGK Đại số 10 nâng cao
Hỏi phải lấy điểm M cách B bao nhiêu để tổng ME + MF = l(l là độ dài cho trước)? Biện luận theo l, a, b và c
Bài 58 trang 102 SGK Đại số 10 nâng cao
Với giá trị nào của a thì hai phương trình sau có nghiệm chung:
Bài 57 trang 101 SGK Đại số 10 nâng cao
Tìm các giá trị của m sao cho tổng bình phương hai nghiệm của nó bằng 1.
Bài 56 trang 101 SGK Đại số 10 nâng cao
Ba cạnh của một tam giác vuông có độ dài là 3 số tự nhiên liên tiếp. Tính độ dài của chúng.
Bài 55 trang 101 SGK Đại số 10 nâng cao
Cho phương trình p(x + 1) - 2x = p2 + p - 4. Tìm các giá trị của p để:
Bài 54 trang 101 SGK Đại số 10 nâng cao
Giải và biện luận phương trình: m(mx – 1) = x + 1
Bài 53 trang 101 SGK Đại số 10 nâng cao
Biết rằng phương trình ax2 + bx + c = 0 có một nghiệm kép xo. Hãy chọn mệnh đề đúng trong các mệnh đề sau:
Bài 52 trang 101 SGK Đại số 10 nâng cao
Hệ phương trình sau có thể có nghiệm trong trường hợp nào?
Bài 51 trang 101 SGK Đại số 10 nâng cao
Hãy chọn kết luận đúng trong hai kết luận sau:
Bài 50 trang 101 SGK Đại số 10 nâng cao
Phương trình ax + b = 0 có thể có nghiệm trong những trường hợp nào?

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.