 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 Bài tập ôn tập chương 3
Bài tập ôn tập chương 3
Bài 63 trang 102 SGK Đại số 10 nâng cao
Tìm a, b và c để Parabol y = ax2 + bx + c có đỉnh là 1(1; -4) và đi qua điểm M(2; -3). Hãy vẽ Parabol nhận được.
Đề bài
Tìm a, b và c để Parabol y = ax2 + bx + c có đỉnh là I(1; -4) và đi qua điểm M(2; -3). Hãy vẽ Parabol nhận được.
Phương pháp giải - Xem chi tiết
Sử dụng các kết quả sau:
Đỉnh của Parabol y = ax2 + bx + c là \((- {b \over {2a}};-{\Delta \over {4a}} )\)
\(A(x_0;y_0)\) thuộc Parabol khi và chỉ khi \(y_0 = ax^2_0 + bx_0 + c\)
Lời giải chi tiết
\(I(1, -4)\) là đỉnh của Parabol nên:
\(\left\{ \matrix{
- {b \over {2a}} = 1 \hfill \cr
- 4 = a + b + c \hfill \cr} \right.\)
\(M(2, -3)\) thuộc parabol nên: \(-3 = 4a + 2b + c\)
Ta có hệ:
\(\left\{ \matrix{
2a + b = 0 \hfill \cr
a + b + c = - 4 \hfill \cr
4a + 2b + c = - 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 1 \hfill \cr
b = - 2 \hfill \cr
c = - 3 \hfill \cr} \right.\)
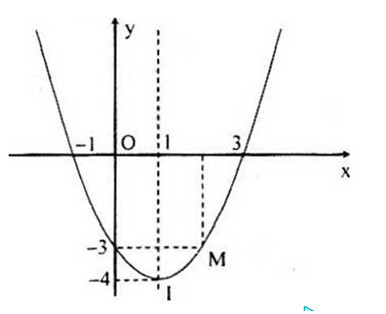
Vậy \(y = x^2 – 2x – 3\)
Đồ thị hàm số: \(y = x^2 – 2x – 3\)
Loigiaihay.com
- Bài 64 trang 102 SGK Đại số 10 nâng cao
- Bài 62 trang 102 SGK Đại số 10 nâng cao
- Bài 61 trang 102 SGK Đại số 10 nâng cao
- Bài 60 trang 102 SGK Đại số 10 nâng cao
- Bài 59 trang 102 SGK Đại số 10 nâng cao
>> Xem thêm



















