 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Bài 4. Một số phương pháp tích phân
Bài 4. Một số phương pháp tích phân
Bài 20 Trang 161 SGK Đại số và Giải tích 12 Nâng cao
Tính
Tính
LG a
\(\int\limits_0^\pi {5{{\left( {5 - 4\cos t} \right)}^{{1 \over 4}}}} \sin tdt;\)
Lời giải chi tiết:
Đặt \(u = 5 - 4\cos t \Rightarrow du = 4\sin tdt \) \(\Rightarrow \sin tdt = {1 \over 4}du\)
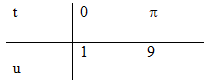
\(\int\limits_0^\pi {5{{\left( {5 - 4\cos t} \right)}^{{1 \over 4}}}} \sin tdt\) \( = \dfrac{5}{4}.\left. {\dfrac{{{u^{\frac{1}{4} + 1}}}}{{\frac{1}{4} + 1}}} \right|_1^9\) \( = {5 \over 4}\int\limits_1^9 {{u^{{1 \over 4}}}du = \left. {{u^{{5 \over 4}}}} \right|} _1^9 = {9^{{5 \over 4}}} - 1\)
LG b
\(\int\limits_0^{\sqrt 3 } {{{{x^3}dx} \over {\sqrt {{x^2} + 1} }}} .\)
Lời giải chi tiết:
Đặt \(\displaystyle u = \sqrt {{x^2} + 1} \Rightarrow {u^2} = {x^2} + 1 \) \(\displaystyle \Rightarrow udu = xdx \) \(\displaystyle \Rightarrow {x^3}dx = {x^2}.xdx = \left( {{u^2} - 1} \right)udu\)
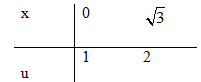
\(\displaystyle \int\limits_0^{\sqrt 3 } {{{{x^3}dx} \over {\sqrt {{x^2} + 1} }}} = \int\limits_1^2 {{{\left( {{u^2} - 1} \right)u} \over u}} du\)
\(\displaystyle \int\limits_1^2 {\left( {{u^2} - 1} \right)du} = \left. {\left( {{{{u^3}} \over 3} - u} \right)} \right|_1^2\) \(\displaystyle = \frac{8}{3} - 2 - \frac{1}{3} + 1\) \(\displaystyle = {4 \over 3}\)
Loigiaihay.com
- Bài 21 Trang 161 SGK Đại số và Giải tích 12 Nâng cao
- Bài 22 Trang 162 SGK Đại số và Giải tích 12 Nâng cao
- Bài 23 Trang 162 SGK Đại số và Giải tích 12 Nâng cao
- Bài 24 Trang 162 SGK Đại số và Giải tích 12 Nâng cao
- Bài 25 Trang 162 SGK Đại số và Giải tích 12 Nâng cao
>> Xem thêm


















