Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi H là chân đường vuông góc hạ từ O đến mặt phẳng (ABC). Chứng minh rằng:
a) H là trực tâm của tam giác ABC.
b) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
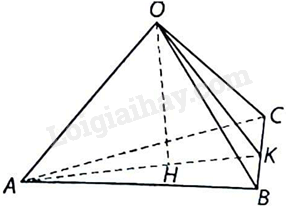
a) Vì \(OA \bot OB,OA \bot OC\) và OB và OC cắt nhau tại O và nằm trong mặt phẳng (OBC) nên \(OA \bot \left( {OBC} \right)\). Mà \(BC \subset \left( {OBC} \right) \Rightarrow OA \bot BC\)
Vì \(OH \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow OH \bot BC\)
Ta có: \(OH \bot BC,OA \bot BC\), OA và OH cắt nhau tại O và nằm trong mặt phẳng (OAH).
Do đó, \(BC \bot \left( {OAH} \right)\). Mà \(AH \subset \left( {OAH} \right) \Rightarrow BC \bot AH\).
Chứng minh tương tự ta có: \(CA \bot BH\).
Tam giác ABC có hai đường cao AH và BH cắt nhau tại H nên H là trực tâm của tam giác ABC.
b) Gọi K là giao điểm của AH và BC.
Khi đó, \(OK \bot BC\left( {do\;BC \bot \left( {OAH} \right)} \right),\) \(OA \bot OK\left( {do\;OA \bot \left( {OBC} \right)} \right)\)
Suy ra OK là đường cao của tam giác vuông OBC và OH là đường cao của tam giác vuông OAK.
Áp dụng hệ thức lượng trong các tam giác vuông OBC vuông tại O và OAK vuông tại O ta có: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{K^2}}}\) và \(\frac{1}{{O{K^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Do đó, \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{K^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Các bài tập cùng chuyên đề
Cho hàm số: \(y = \ln \left[ {\left( {{m^2} + 4m - 5} \right){x^2} - 2\left( {m - 1} \right)x + 2} \right]\).
a) Với \(m = 1\), hãy tìm tập xác định của hàm số trên.
b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định với mọi giá trị thực của x.
Cho phương trình \(3{\log _8}\left[ {2{x^2} - \left( {m + 3} \right)x + 1 - m} \right] + {\log _{\frac{1}{2}}}\left( {{x^2} - x + 1 - 3m} \right) = 0\) (m là tham số). Có bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn \(\left| {{x_1} - {x_2}} \right| < 15\)?






