Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Ôn tập chương III : Quan hệ giữa các yếu tố trong tam g..
Bài 63 trang 87 SGK Toán 7 tập 2
Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB.
Đề bài
Cho tam giác \(ABC\) với \(AC < AB.\) Trên tia đối của tia \(BC\) lấy điểm \(D\) sao cho \(BD = AB.\) Trên tia đối của tia \(CB\) lấy điểm \(E\) sao cho \(CE = AC.\) Vẽ các đoạn thẳng \(AD, AE.\)
a) Hãy so sánh góc \(ADC\) và góc \(AEB.\)
b) Hãy so sánh các đoạn thẳng \(AD\) và \(AE.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng quan hệ giữa góc và cạnh đối diện trong tam giác.
Lời giải chi tiết
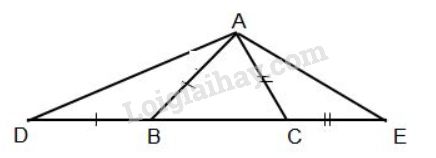
a) Xét \(ΔABC\) có \(AC < AB\) (giả thiết)
\(⇒ \widehat {ABC} < \widehat {ACB}\) (quan hệ giữa cạnh và góc đối diện trong tam giác) (1)
\(ΔABD\) cân tại \(B\) vì \(AB = BD\) (giả thiết)
\(⇒ \widehat {ADB} = \widehat {DAB}\) (tính chất)
Mà \(\widehat {ABC} = \widehat {ADB} + \widehat {DAB}\) (góc ngoài tam giác)
⇒ \(\widehat {DAB} = \widehat {ADB} = \dfrac{\widehat {ABC}}{2} \) (2)
\(ΔACE\) cân tại \(C\) vì \(CA = CE\) (giả thiết)
\(⇒ \widehat {CAE} = \widehat {CEA}\) (tính chất)
Mà \(\widehat {ACB} = \widehat {CAE} + \widehat {CEA}\) (góc ngoài tam giác)
⇒ \(\widehat {CAE} = \widehat {CEA} = \dfrac{\widehat {ACB}}{2}\) (3)
Từ (1), (2), (3) suy ra \(\widehat {ADB} < \widehat {AEC}\)
hay \(\widehat {ADC} < \widehat {AEB}\) (điều phải chứng minh).
b) Xét \(ΔADE\) có \(\widehat {ADE} < \widehat {AED}\) (chứng minh ở phần a)
Mà \(AE\) là cạnh đối diện \(\widehat {ADE}\) và \(AD\) là cạnh đối diện \(\widehat {AED}\)
\( \Rightarrow AE < AD\) (Quan hệ giữa góc - cạnh đối diện trong tam giác).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 64 trang 87 SGK Toán 7 tập 2
- Bài 65 trang 87 SGK Toán 7 tập 2
- Bài 66 trang 87 SGK Toán 7 tập 2
- Bài 67 trang 87 SGK Toán 7 tập 2
- Bài 68 trang 88 SGK Toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
