Cho a, b, m là các số nguyên, m khác 0. Tổng \(\frac{a}{m} + \frac{b}{m}\) bằng
-
A.
\(\frac{{a + b}}{{m + m}}\).
-
B.
\(\frac{{a + b}}{{m.m}}\).
-
C.
\(\frac{{a + b}}{m}\).
-
D.
\(a + b\).
Dựa vào quy tắc cộng hai phân số cùng mẫu.
\(\frac{a}{m} + \frac{b}{m} = \frac{{a + b}}{m}\)
Đáp án C.
Đáp án : C
Các bài tập cùng chuyên đề
Phân số nghịch đảo của phân số \(\frac{1}{3}\) là
Khẳng định nào sau đây đúng?
Cho \(\frac{3}{4}x = 1\frac{2}{3}\). Kết quả giá trị x là:
Trong các cách viết sau, cách viết nào cho ta một số thập phân âm?
Số đối của số thập phân -3,7 là:
Làm tròn số 12,643 đến hàng đơn vị ta được số
Tỉ số phần trăm của 1 và 4 là
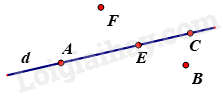
Cho hình vẽ: Điểm thuộc đường thẳng d là:
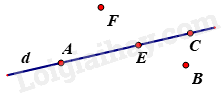
Cho hình vẽ, chọn khẳng định đúng trong các khẳng định sau:
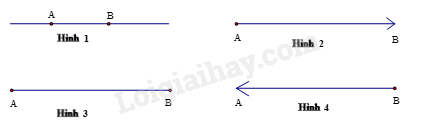
Hình nào sau đây vẽ đoạn thẳng \(AB\)?
Cho \(I\) là trung điểm của đoạn thẳng \(AB\). Biết \(AB = 10cm\), số đo của đoạn thẳng \(IB\) là
Thực hiện các phép tính sau (tính hợp lý nếu có thể).
a) \(\frac{{ - 2}}{{11}} + \frac{{ - 9}}{{11}}\)
b) \(\frac{1}{2} - \frac{{ - 3}}{4}\)
c) \(\frac{{12}}{{11}} - \frac{{ - 7}}{{19}} + \frac{{12}}{{19}}\)
d) \(\frac{{ - 5}}{7} \cdot \frac{2}{{11}} + \frac{{ - 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7}\)
Tìm \(x\), biết:
a) \(2,5 + x = 3,75\)
b) \(6,72 - x = ( - 12,6) + 6,3\)
Lớp 6A có 42 học sinh xếp loại kết quả học tập trong học kỳ I bao gồm ba loại: Tốt, khá và đạt. Số học sinh tốt chiếm \(\frac{1}{7}\) số học sinh cả lớp, số học sinh khá bằng \(\frac{2}{3}\) số học sinh còn lại.
a) Tính số học sinh mỗi loại của lớp?
b) Tính tỉ số phần trăm của số học sinh tốt và khá so với số học sinh cả lớp?
Trên tia Bx lấy hai điểm A và C sao cho BA = 2cm , BC = 3cm
a) Trong ba điểm C, A, B điểm nào nằm giữa hai điểm còn lại? Tính AC?
b) Trên tia đối của tia Bx lấy điểm O sao cho BO = BC = B có phải là trung điểm của OC không? Vì sao?
Tính \(S = \left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)\left( {1 - \frac{1}{{{4^2}}}} \right)\left( {1 - \frac{1}{{{5^2}}}} \right)\left( {1 - \frac{1}{{{6^2}}}} \right)...\left( {1 - \frac{1}{{{{99}^2}}}} \right)\).






