Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp

Đề kiểm tra 15 phút - Đề số 2 - Bài 8 - Chương 3 - Hình học 9


Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 8 - Chương 3 - Hình học 9

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Đề bài

Cho đường tròn (O; R). Vẽ tam giác đều nội tiếp và hãy tính cạnh của tam giác theo R.

Phương pháp giải - Xem chi tiết

Sử dụng:

+Tâm đường tròn ngoại tiếp tam giác đều trùng với trọng tâm tam giác. 

+Tỉ số lượng giác của góc nhọn

Lời giải chi tiết

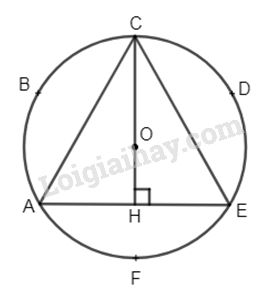
Trên đường tròn (O; R) lấy lần lượt các dây cung \(AB= BC = CD = DE = EF = FA\)\(\, (=R)\)

Nối A với C, C với E, E với A, ta được \(AC = CE = EA\).

Do đó \(∆ACE\) đều.

Ta đã biết : Tâm đường tròn ngoại tiếp tam giác đều trùng với trọng tâm tam giác. Ta có :

\(CH = CO + OH = R + \dfrac{R }{ 2}\) ( tính chất trọng tâm)

\(\;\;\;\;\;\;\; = \dfrac{{3R} }{ 2}\)

∆AHC vuông ta có :

\(AH = CH.\cot A = \dfrac{{3R} }{ 2}.\cot 60^\circ  \)\(\,= \dfrac{{3R} }{2}.\dfrac{1}{ {\sqrt 3 }} = \dfrac{{R\sqrt 3 } }{ 2}\)

\( \Rightarrow AE = R\sqrt 3 .\)      

Vậy cạnh của tam giác đều nội tiếp đường tròn (O; R) là \(R\sqrt 3 .\)

Loigiaihay.com


Bình chọn:
4.3 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K9 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com, cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua