Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 1. Một số hệ thức về cạnh và đường cao trong tam gi..

Bài 9 trang 70 SGK Toán 9 tập 1


Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B.

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Cho hình vuông \(ABCD\). Gọi \(I\) là một điểm nằm giữa \(A\) và \(B\). Tia \(DI\) và tia \(CB\) cắt nhau ở \(K\). Kẻ đường thẳng qua \(D\), vuông góc với \(DI\). Đường thẳng này cắt đường thẳng \(BC\) tại \(L\). Chứng minh rằng:

a) Tam giác \(DIL\) là một tam giác cân;

b) Tổng \(\dfrac{1}{DI^{2}}+\dfrac{1}{DK^{2}}\) không đổi khi \(I\) thay đổi trên cạnh \(AB\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Chứng minh hai tam giác bằng nhau\((\Delta{ADI}\) và \(\Delta{CDL})\) từ đó suy ra hai cạnh tương ứng bằng nhau.

b) Sử dụng hệ thức lượng trong tam giác vuông: \(\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\) để đưa tổng đã cho về tổng của các số không đổi.

Lời giải chi tiết

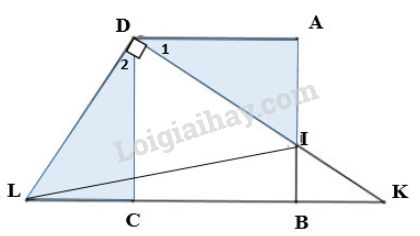
a) Xét \(\Delta ADI\) và \(\Delta CDL\) có: 

               \(\widehat{A}=\widehat{C}= 90^{\circ}\)

              \(AD=CD\) (hai cạnh hình vuông)

             \(\widehat{D_{1}}=\widehat{D_{2}}\)  (cùng phụ với \(\widehat{CDI})\)

Do đó \(\Delta ADI=\Delta CDL\) (g.c.g)

\(\Rightarrow DI=DL\) ( 2 cạnh tương ứng)

Vậy \(\Delta DIL\) cân tại D (đpcm).

b) Xét \(\Delta{DLK}\) vuông tại \(D\), đường cao \(DC\).

Áp dụng hệ thức lượng \(\dfrac{1}{h^{2}}=\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}\) trong tam giác vuông DKL, đường cao DC, ta có:

                 \(\dfrac{1}{DC^{2}}=\dfrac{1}{DL^{2}}+\dfrac{1}{DK^{2}}\)  (mà \(DL=DI)\)

\(\Rightarrow \dfrac{1}{DC^{2}}=\dfrac{1}{DI^{2}}+\dfrac{1}{DK^{2}}\)

Do ABCD cố định nên \(DC\) không đổi, do đó \(\dfrac{1}{DI^{2}}+\dfrac{1}{DK^{2}}\) là không đổi.

Chú ý: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức \(\dfrac{1}{h^{2}}=\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}\)

Nếu đề bài không cho gợi ý vẽ \(DL\perp DK\) thì ta vẫn phải kẻ thêm đường nét phụ \(DL\perp DK\) để có thể vận dụng hệ thức trên.


Bình chọn:
4.7 trên 196 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store