 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Bài 3. Các hệ thức lượng trong tam giác và giải tam giác
Bài 3. Các hệ thức lượng trong tam giác và giải tam giác
Bài 9 trang 59 SGK Hình học 10
Cho hình bình hành ABCD có
Đề bài
Cho hình bình hành \(ABCD\) có \(AB = a, BC = b ,BD = m\), và \(AC = n\). Chứng minh rằng :
$${m^2} + {n^2} = 2({a^2} + {b^2})$$
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Công thức đường trung tuyến: \( m_a^2=\frac{2(b^2+c^2)-a^2}{4}.\)
Lời giải chi tiết
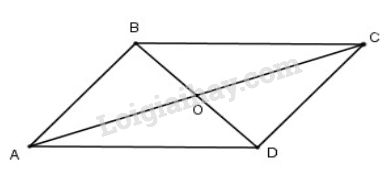
Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và BD.
Tam giác ABD có AO là đường trung tuyến.
Áp dụng định lí về đường trung tuyến:
\(A{O^2} = \frac{{2\left( {A{B^2} + A{D^2}} \right) - B{D^2}}}{4}\)
Mà O là trung điểm AC nên \(AO = \frac{{AC}}{2} = \frac{n}{2}\)
Thay \(OA = \frac{n}{2}, \, AB = a,\) \(AD = BC = b\) và \(BD = m\) ta được:
\(\begin{array}{l}
{\left( {\frac{n}{2}} \right)^2} = \frac{{2\left( {{a^2} + {b^2}} \right) - {m^2}}}{4}\\
\Leftrightarrow \frac{{{n^2}}}{4} = \frac{{2\left( {{a^2} + {b^2}} \right) - {m^2}}}{4}\\
\Leftrightarrow {n^2} = 2\left( {{a^2} + {b^2}} \right) - {m^2}\\
\Leftrightarrow {m^2} + {n^2} = 2\left( {{a^2} + {b^2}} \right)
\end{array}\)
Cách 2:
Áp dụng định lý đường trung tuyến cho tam giác ABC có BO là đường trung tuyến ra có:
\(\begin{array}{l}
B{O^2} = \frac{{2\left( {B{A^2} + B{C^2}} \right) - A{C^2}}}{4}\\
\Leftrightarrow {\left( {\frac{m}{2}} \right)^2} = \frac{{2\left( {{a^2} + {b^2}} \right) - {n^2}}}{4}\\
\Leftrightarrow \frac{{{m^2}}}{4} = \frac{{2\left( {{a^2} + {b^2}} \right) - {n^2}}}{4}\\
\Leftrightarrow {m^2} = 2\left( {{a^2} + {b^2}} \right) - {n^2}\\
\Leftrightarrow {m^2} + {n^2} = 2\left( {{a^2} + {b^2}} \right)
\end{array}\)
Cách 3:
Áp dụng định lí cô sin cho tam giác ABC có:
\(\begin{array}{l}
A{C^2} = A{B^2} + B{C^2} - 2AB.BC\cos \widehat {ABC}\\
\Rightarrow {n^2} = {a^2} + {b^2} - 2ab\cos \widehat {ABC}
\end{array}\)
Áp dụng định lí cô sin cho tam giác ABD có:
\(\begin{array}{l}
B{D^2} = A{B^2} + A{D^2} - 2AB.AD\cos \widehat {BAD}\\
\Rightarrow {m^2} = {a^2} + {b^2} - 2ab\cos \widehat {BAD}
\end{array}\)
\(\begin{array}{l}
\Rightarrow {m^2} + {n^2}\\
= \left( {{a^2} + {b^2}} \right) - 2ab\cos \widehat {ABC}\\
+ \left( {{a^2} + {b^2}} \right) - 2ab\cos \widehat {BAD}\\
= 2\left( {{a^2} + {b^2}} \right) - 2ab\left( {\cos \widehat {ABC} + \cos \widehat {BAD}} \right)
\end{array}\)
Mà \(\widehat {ABC} + \widehat {BAD} = {{180}^0} \) \( \Rightarrow \cos \widehat {ABC} = - \cos \left( {{{180}^0} - \widehat {ABC}} \right) \) \(= - \cos \widehat {BAD}\)
\( \Rightarrow \cos \widehat {ABC} + \cos \widehat {BAD} = 0\)
Vậy \({m^2} + {n^2} = 2\left( {{a^2} + {b^2}} \right)\).
Loigiaihay.com
- Bài 10 trang 60 SGK Hình học 10
- Bài 11 trang 60 SGK Hình học 10
- Bài 8 trang 59 SGK Hình học 10
- Bài 7 trang 59 SGK Hình học 10
- Bài 6 trang 59 SGK Hình học 10
>> Xem thêm



















