Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 12. Hình vuông

Bài 85 trang 109 SGK Toán 8 tập 1


Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE

Đề bài

Cho hình chữ nhật \(ABCD\) có \(AB = 2AD\).  Gọi \(E, F\) theo thứ tự là trung điểm của \(AB, CD\). Gọi \(M\) là giao điểm của \(AF\) và \(DE\), \(N\) là giao điểm của \(BF\) và \(CE\).

a) Tứ giác \(ADFE\) là hình gì? Vì sao?

b) Tứ giác \(EMFN\) là hình gì? Vì sao?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Áp dụng dấu hiệu nhận biết:

- Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành,

- Tứ giác có các cặp cạnh đối song song là hình bình hành,

- Hình bình hành có một góc vuông là hình chữ nhật,

- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Lời giải chi tiết

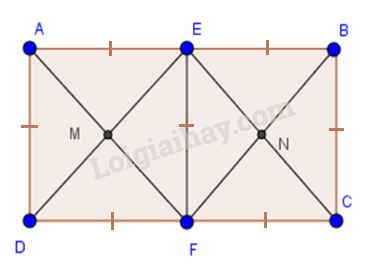
Vì \(ABCD\) là hình chữ nhật nên \(AB=CD,AD=BC, AB//CD\)

Lại có \(E, F\) theo thứ tự là trung điểm của \(AB, CD\) nên \(AE=EB=\dfrac{AB}2\), \(DF=FC=\dfrac{DC}2\)

Lại có \(AB=2AD\) 

Suy ra \(AE = EB = BC = CF = FD = DA\)

a) Xét tứ giác \(ADFE\) có:

\(AE // DF\) (do \(AB//CD\)), \(AE = DF\) (chứng minh trên)

\( \Rightarrow \) Tứ giác \(ADFE\) là hình bình hành (dấu hiệu nhận biết hình bình hành)

Hình bình hành \(ADFE\) có \(\widehat{A} = 90^0\) nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật )

Hình chữ nhật \(ADFE\) có \(AE = AD\) (chứng minh trên) nên nó là hình vuông (dấu hiệu nhận biết hình vuông)

b) Xét tứ giác \(DEBF\) có:

\(EB // DF\) (do \(AB//CD\)),  \(EB = DF\) (chứng minh trên)

\( \Rightarrow \) Tứ giác \(DEBF\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

\( \Rightarrow \) \(DE // BF\) (tính chất hình bình hành)

Xét tứ giác \(AECF\) có:

\(EA // CF\) (do \(AB//CD\)), \(EA = CF\) (chứng minh trên)

\( \Rightarrow \) Tứ giác \(AECF\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

\( \Rightarrow \) \(AF // EC\) (tính chất hình bình hành)

Xét tứ giác \(EMFN\) có: \(ME//NF,MF//NE\) (do \(DE // BF,AF//EC \) (chứng minh trên))

\( \Rightarrow \) Tứ giác \(EMFN\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

Theo câu a, \(ADFE\) là hình vuông nên \(ME = MF, ME  ⊥ MF\) (tính chất hình vuông)

Hình bình hành \(EMFN\) có \(\widehat{M} = 90^0\) nên là hình chữ nhật, lại có \(ME = MF\) nên là hình vuông (dấu hiệu nhận biết hình vuông)

Loigiaihay.com


Bình chọn:
4.4 trên 261 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua