 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Ôn tập chương I: Phép nhân và phép chia các đa thức
Ôn tập chương I: Phép nhân và phép chia các đa thức
Bài 83 trang 33 SGK Toán 8 tập 1
Tìm n để phân thức chia hết cho 2n +1.
Đề bài
Tìm \(n \in\mathbb Z\) để \(2{n^2} - n + 2\) chia hết cho \(2n +1\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Thực hiện phép chia \((2{n^2} - n + 2) :(2n +1)\) để tìm số dư, sau đó để phép chia là phép chia hết thì số dư phải chia hết cho \(2n+1\).
Lời giải chi tiết
Thực hiện phép chia \(2n^2 – n + 2\) cho \(2n + 1\) ta có:
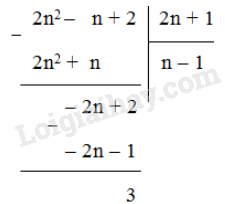
Để \(2n^2 – n + 2\) chia hết cho \(2n + 1\) thì \(3\) chia hết cho \(2n+1\)
Suy ra \(2n + 1\) phải là ước của \(3\), hay \( 2n+1 \in \{1;\;-1;\; 3;\; -3\} \).
+) \(2n + 1 = 1 \Rightarrow 2n = 0 \Rightarrow n = 0\)
+) \(2n + 1 = - 1 \Rightarrow 2n = - 2 \Rightarrow n = - 1\)
+) \(2n + 1 = 3 \Rightarrow 2n = 2 \Rightarrow n = 1\)
+) \(2n + 1 = - 3 \Rightarrow 2n = - 4 \Rightarrow n = - 2\)
Vậy \(n \in \{ \;-2; -1;0\,;\; 1\}\)
Cách khác:
Ta có:
\(\eqalign{
& {{2{n^2} - n + 2} \over {2n + 1}} \cr
& = {{2{n^2} + n - 2n - 1 + 3} \over {2n + 1}} \cr
& = {{\left( {2{n^2} + n} \right) + \left( { - 2n - 1} \right) + 3} \over {2n + 1}} \cr
& = {{n\left( {2n + 1} \right) - \left( {2n + 1} \right) + 3} \over {2n + 1}} \cr
& = {{\left( {2n + 1} \right)\left( {n - 1} \right) + 3} \over {2n + 1}} \cr
& = n - 1 + {3 \over {2n + 1}} \cr} \)
Để \(2{n^2} - n + 2\) chia hết cho \(2n + 1\) (với \(n \in\mathbb Z)\) thì \(3\) chia hết cho \(2n+1\)
Suy ra, \(2n + 1\) phải là ước của \(3\), hay \( 2n+1 \in \{1;\;-1;\; 3;\; -3\} \).
+) \(2n + 1 = 1 \Rightarrow 2n = 0 \Rightarrow n = 0\)
+) \(2n + 1 = - 1 \Rightarrow 2n = - 2 \Rightarrow n = - 1\)
+) \(2n + 1 = 3 \Rightarrow 2n = 2 \Rightarrow n = 1\)
+) \(2n + 1 = - 3 \Rightarrow 2n = - 4 \Rightarrow n = - 2\)
Vậy \(n \in \{ \;-2; -1;0\,;\; 1\}\)
Loigiaihay.com
- Lý thuyết Ôn tập chương 1. Phép nhân và phép chia các đa thức
- Đề kiểm tra 45 phút ( 1 tiết) - Đề số 1 - Chương 1 - Đại số 8
- Đề kiểm tra 45 phút ( 1 tiết) - Đề số 2 - Chương 1 - Đại số 8
- Đề kiểm tra 45 phút ( 1 tiết) - Đề số 3 - Chương 1 - Đại số 8
- Đề kiểm tra 45 phút ( 1 tiết) - Đề số 4 - Chương 1 - Đại số 8
>> Xem thêm

















