Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Bài 2. Phương trình lượng giác cơ bản

Giải bài 7 trang 29 SGK Đại số và Giải tích 11


Giải các phương trình sau:

Video hướng dẫn giải

Lựa chọn câu để xem lời giải nhanh hơn

Giải các phương trình sau:

LG a

\(\begin{array}{l}\,\,\sin 3x - \cos 5x = 0\\\end{array}\)

Phương pháp giải:

B1: chuyển vế, đưa PT về dạng \(sin \alpha= cos \beta\).

B2: Do \(\sin x = \cos \left( {\frac{\pi }{2} - x} \right)\) PT trở về dạng \(\cos X = \cos Y \) với \(X=\left( {\frac{\pi }{2} - x} \right); Y= \beta\)

\(\Leftrightarrow \left[ \begin{array}{l}X =Y + k2\pi \\ X = - Y + k2\pi \end{array} \right.\,\,\left( {k \in Z} \right)\)

Từ đó suy ra nghiệm x và KL.

Lời giải chi tiết:

\(\begin{array}{l}\,\,\sin 3x - \cos 5x = 0\\\Leftrightarrow \cos 5x=\sin 3x = \cos \left( {\frac{\pi }{2} - 3x} \right)\\\Leftrightarrow \left[ \begin{array}{l}5x = \frac{\pi }{2} - 3x + k2\pi \\5x = - \frac{\pi }{2} + 3x + k2\pi \end{array} \right.\\\Leftrightarrow \left[ \begin{array}{l}8x = \frac{\pi }{2} + k2\pi \\2x = - \frac{\pi }{2} + k2\pi \end{array} \right.\\\Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}\\x = - \frac{\pi }{4} + k\pi \end{array} \right.\,\,\,\left( {k \in Z} \right)\end{array}\)

Vậy nghiệm phương trình là: \(x=\frac{\pi }{16}+\frac{k\pi }{4} (k\in Z)\) và \(x=-\frac{\pi }{4} +k\pi, (k\in \mathbb{Z})\)

Cách khác:

sin3x - cos5x = 0

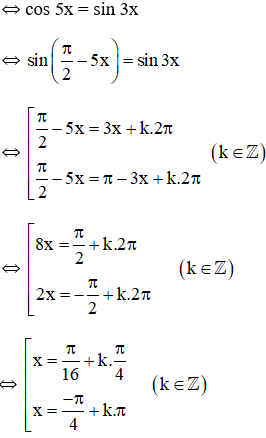
Vậy nghiệm phương trình là: \(x=\frac{\pi }{16}+\frac{k\pi }{4} (k\in Z)\) và \(x=-\frac{\pi }{4} +k\pi, (k\in \mathbb{Z})\)

LG b

\(\begin{array}{l}\,\,\tan 3x\tan x = 1\end{array}\)

Phương pháp giải:

B1: Tìm ĐKXĐ.

B2: vì \(\frac{1}{{\tan x}} = \cot x = \tan \left( {\frac{\pi }{2} - x} \right)\)

phương trình trở về dạng \(\tan \alpha  = \tan \beta  \) với \(\alpha = 3x; \beta =\frac{\pi }{2} - x\)

\(\Leftrightarrow \alpha  = \beta  + k\pi \,\,\left( {k \in Z} \right)\)

B3: Suy ra nghiệm x rồi KL.

Lời giải chi tiết:

Điều kiện:

\(\begin{array}{l}\left\{ \begin{array}{l}\cos 3x \ne 0\\\cos x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x \ne \frac{\pi }{2} + k\pi \\x \ne \frac{\pi }{2} + k\pi \end{array} \right.\\\Leftrightarrow \left\{ \begin{array}{l}x \ne \frac{\pi }{6} + \frac{{k\pi }}{3}\\x \ne \frac{\pi }{2} + k\pi \end{array} \right. \Rightarrow x \ne \frac{\pi }{6} + \frac{{k\pi }}{3}\,\,\left( {k \in Z} \right)\end{array}\)

\(\begin{array}{l}\tan 3x\tan x = 1\\\Leftrightarrow \tan 3x = \frac{1}{{\tan x}} \\ \Leftrightarrow \tan 3x = \cot x \\ \Leftrightarrow \tan 3x = \tan \left( {\frac{\pi }{2} - x} \right)\\ \Leftrightarrow 3x = \frac{\pi }{2} - x + k\pi \\\Leftrightarrow 4x = \frac{\pi }{2} + k\pi \\\Leftrightarrow x = \frac{\pi }{8} + \frac{{k\pi }}{4}\,\,\,\left( {k \in Z} \right)\,\,\,\left( {tm} \right)\end{array}\)

Vậy nghiệm phương trình là \(x=\frac{\pi }{8}+\frac{k \pi }{4}, \)\(k \in \mathbb{Z}\).

Chú ý:

Ở bài này ta thấy ngay họ nghiệm \(x=\frac{\pi }{8}+\frac{k \pi }{4}, k \in \mathbb{Z}\) không có nghiệm nào vi phạm điều kiện xác định nên ta lấy cả họ nghiệm và không phải loại bỏ điểm nào.

Loigiaihay.com


Bình chọn:
4.6 trên 51 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua