Bài 7 trang 12 SGK Hình học 10
Cho , là hai vectơ khác. Khi nào có đẳng thức
Video hướng dẫn giải
Cho \(\overrightarrow{a}\), \(\overrightarrow{b}\) là hai vectơ khác\(\overrightarrow{0}\). Khi nào có đẳng thức
LG a
\(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} \right |\) + \(\left | \overrightarrow{b} \right |\);
Phương pháp giải:
Với quy tắc ba điểm tùy ý \(A, \, \, B, \, \, C\) ta luôn có:
\(+ )\;\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (quy tắc ba điểm).
\( + )\;\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \) (quy tắc trừ).
Lời giải chi tiết:
Xét: \(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} \right |\) + \(\left | \overrightarrow{b} \right |\)
Dựng hình bình hành \(ABCD\) sao cho \(\overrightarrow {AB} = \overrightarrow {DC} = \overrightarrow a ,\;\;\overrightarrow {AD} = \overrightarrow {BC} = \overrightarrow b .\)
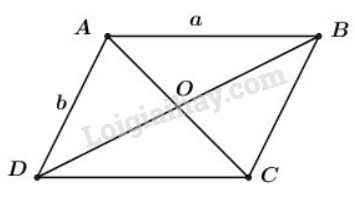
Khi đó ta có: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) \( \Rightarrow \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow {AC} } \right| = AC.\)
Lại có: \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \) \(= \left| {\overrightarrow {AB} } \right| + \left| {\overrightarrow {BC} } \right| = AB + BC\)
Suy ra \( \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)\( \Leftrightarrow AC = AB + BC\)
\( \Leftrightarrow\) 3 điểm \( A, \, \, B,\, \, C\) thẳng hàng và \(B\) nằm giữa \(A, \, \, C\)
\( \Rightarrow \overrightarrow {AB} ,\overrightarrow {BC} \) cùng hướng
Hay \(\overrightarrow a ,\;\overrightarrow b \) cùng hướng.
Vậy \(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} \right |+ \left | \overrightarrow{b} \right |\) khi hai vectơ \(\overrightarrow{a}, \, \, \overrightarrow{b}\) cùng hướng.
LG b
\(\left | \overrightarrow{a}+\overrightarrow{b} \right |= \left | \overrightarrow{a}-\overrightarrow{b} \right |\).
Phương pháp giải:
Với quy tắc ba điểm tùy ý \(A, \, \, B, \, \, C\) ta luôn có:
\(+ )\;\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (quy tắc ba điểm).
\( + )\;\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \) (quy tắc trừ).
Lời giải chi tiết:
Xét \(\left | \overrightarrow{a}+\overrightarrow{b} \right |= \left | \overrightarrow{a}-\overrightarrow{b} \right |.\)
Tương tự câu a ta có: \( \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow {AC} } \right| = AC.\)
Ta có: \(\overrightarrow a - \overrightarrow b = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \) \( \Rightarrow \left| {\overrightarrow a - \overrightarrow b } \right| = \left| {\overrightarrow {DB} } \right| = DB.\)
\( \Rightarrow \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a - \overrightarrow b } \right| \)\(\Leftrightarrow AC = DB.\)
Khi đó hình bình hành \(ABCD\) là hình chữ nhật \(\Rightarrow AB \perp BC\) hay \(\overrightarrow{a}\perp\overrightarrow{b}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 8 trang 12 SGK Hình học 10
- Bài 9 trang 12 SGK Hình học 10
- Bài 10 trang 12 SGK Hình học 10
- Bài 6 trang 12 SGK Hình học 10
- Bài 5 trang 12 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
