Bài 6 trang 9 SGK Toán 8 tập 2

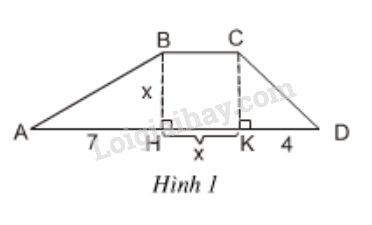
Tính diện tích của hình thang ABCD (h.1) theo x bằng hai cách:

Đề bài

Tính diện tích của hình thang \(ABCD\) (h.1) theo \(x\) bằng hai cách:

1) Tính theo công thức \(S = BH \times (BC + DA) : 2\);

2) \(S = {S_{ABH}} + {S_{BCKH}} + {S_{CKD}}\)

Sau đó sử dụng giả thiết \(S = 20\) để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Phương trình có dạng \(ax+b=0\), với \(a\) và \(b\) là hai số đã cho và \(a\ne0\), được gọi là phương trình bậc nhất một ẩn.

Lời giải chi tiết

Gọi S là diện tích hình thang ABCD.

1) Theo công thức

\(S = \dfrac{BH(BC+DA)}{2}\)

Ta có: \(AD = AH + HK + KD\)

\(\Rightarrow AD = 7 + x + 4 = 11 + x\)

Có \(BH\bot HK, CK\bot HK\) (giả thiết)

Mà \(BC//HK\) (vì \(ABCD\) là hình thang)

Do đó \(BH\bot BC, CK\bot BC\)

Tứ giác \(BCKH\) có bốn góc vuông nên \(BCKH\) là hình chữ nhật

Mặt khác: \(BH=HK=x\) (giả thiết) nên \(BCKH\) là hình vuông

\( \Rightarrow BH = BC =CK=KH= x\)

Thay \(BH=x\), \(BC=x\), \(DA=11+x\) vào biểu thức tính \(S\) ta được:

\(S = \dfrac{{x\left( {x + 11 + x} \right)}}{2} = \dfrac{{x(11 + 2x)}}{2}\)\(\,=\dfrac{{11x + 2{x^2}}}{2}\)

2) Ta có:

\(\eqalign{
& S = {S_{ABH}} + {S_{BCKH}} + {S_{CKD}} \cr
& \,\,\,\,\, = {1 \over 2}BH.AH + BH.HK + {1 \over 2}CK.KD \cr
& \,\,\,\,\, = {1 \over 2}x.7 + x.x + {1 \over 2}.x.4 \cr
& \,\,\,\,\, = {7 \over 2}x + {x^2} + 2x \cr
& \,\,\,\,\, =x^2+{11 \over 2}x \cr} \)

Vậy \(S = 20\) ta có hai phương trình:

\(\dfrac{{11x + 2{x^2}}}{2}= 20\) (1)

\( \dfrac{11}{2}x + x^2 = 20 \) (2)

Hai phương trình trên tương đương và cả hai phương trình không có phương trình nào là phương trình bậc nhất.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 294 phiếu

Bài tiếp theo

Bài 7 trang 10 SGK Toán 8 tập 2
Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau:
Bài 8 trang 10 SGK Toán 8 tập 2
Giải bài 8 trang 10 SGK Toán 8 tập 2. Giải các phương trình:
Bài 9 trang 10 SGK Toán 8 tập 2
Giải bài 9 trang 10 SGK Toán 8 tập 2. Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm:
Trả lời câu hỏi 3 Bài 2 trang 9 SGK Toán 8 Tập 2
Trả lời câu hỏi 3 Bài 2 trang 9 SGK Toán 8 Tập 2. Giải phương trình: -0,5x + 2,4 = 0.
Trả lời câu hỏi 2 Bài 2 trang 8 SGK Toán 8 Tập 2
Trả lời câu hỏi 2 Bài 2 trang 8 SGK Toán 8 Tập 2. Giải các phương trình:
Trả lời câu hỏi 1 Bài 2 trang 8 SGK Toán 8 Tập 2
Trả lời câu hỏi 1 Bài 2 trang 8 SGK Toán 8 Tập 2. Giải các phương trình:
Lý thuyết phương trình bậc nhất một ẩn và cách giải
1. Hai quy tắc biến đổi phương trình