Bài 6 trang 69 SGK Toán 9 tập 2
Cho tam giác đều ABC.
Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD
Đề bài
Cho tam giác đều \(ABC\). Gọi \(O\) là tâm của đường tròn đi qua ba đỉnh \(A, B, C\).
a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính \(OA, OB, OC\).
b) Tính số đo các cung tạo bởi hai trong ba điểm \(A, B, C\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng:
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Số đo của cung lớn bằng hiệu giữa \({360^o}\) và số đo của cung nhỏ (có chung hai mút với cung lớn)
Lời giải chi tiết
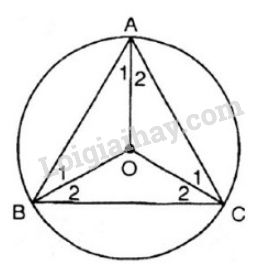
a) Ta có: \(\widehat A = \widehat B = \widehat C = {60^0}\) (gt)
Tâm \(O\) của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều \(ABC\).
Nên \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}} = {30^0}\)
Suy ra: \(\widehat {AOB} = {180^0} - \widehat {{A_1}} - \widehat {{B_1}} = {180^0} - {30^0} - {30^0} = {120^0}\)
Tương tự ta suy ra: \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\)
b) Từ \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\) ta suy ra:
\(sđ\overparen{AB}=sđ\overparen{CA}=sđ\overparen{CB}\) \(= 120^0\)
\(sđ\overparen{ABC}=sđ\overparen{BCA}=sđ\overparen{CAB}\) \(=360^0- 120^0=240^0\)
Loigiaihay.com
- Bài 7 trang 69 SGK Toán 9 tập 2
- Bài 8 trang 70 SGK Toán 9 tập 2
- Bài 9 trang 70 SGK Toán 9 tập 2
- Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 3 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 3 - Hình học 9
>> Xem thêm
Các bài khác cùng chuyên mục




















