-
PHẦN ĐẠI SỐ - TOÁN 9 TẬP 1
-
CHƯƠNG I. CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng Căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo)
- Bài 8. Rút gọn biểu thức chứa căn bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương I – Căn bậc hai. Căn bậc ba
- Đề kiểm tra 15 phút - Chương I - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương I - Đại số 9
-
CHƯƠNG II. HÀM SỐ BẬC NHẤT
- Bài 1. Nhắc lại và bổ sung các khái niệm về hàm số
- Bài 2. Hàm số bậc nhất
- Bài 3. Đồ thị của hàm số y = ax + b (a ≠ 0)
- Bài 4. Đường thẳng song song và đường thẳng cắt nhau
- Bài 5. Hệ số góc của đường thẳng y = ax + b (a ≠ 0).
- Ôn tập chương II – Hàm số bậc nhất
- Đề kiểm tra 15 phút - Chương 2 - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Đại số 9
-
-
PHẦN HÌNH HỌC - TOÁN 9 TẬP 1
-
CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
- Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Bài 2. Tỉ số lượng giác của góc nhọn
- Bài 3. Bảng lượng giác
- Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
- Bài 5. Ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời
- Ôn tập chương I – Hệ thức lượng giác trong tam giác vuông
- Đề kiểm tra 15 phút - Chương 1 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Hình học 9
-
CHƯƠNG II. ĐƯỜNG TRÒN
- Bài 1. Sự xác định của đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương II – Đường tròn
- Đề kiểm tra 15 phút - Chương 2 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 9
-
-
Đề cương ôn tập học kì 1
-
Đề thi học kì 1 mới nhất có lời giải
-
PHẦN ĐẠI SỐ - TOÁN 9 TẬP 2
-
CHƯƠNG III. HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
- Bài 1. Phương trình bậc nhất hai ẩn
- Bài 2. Hệ hai phương trình bậc nhất hai ẩn
- Bài 3. Giải hệ phương trình bằng phương pháp thế
- Bài 4. Giải hệ phương trình bằng phương pháp cộng đại số.
- Bài 5. Giải bài toán bằng cách lập hệ phương trình
- Bài 6. Giải bài toán bằng cách lập hệ phương trình (Tiếp theo)
- Ôn tập Chương III Hệ hai phương trình bậc nhất hai ẩn
- Đề kiểm 15 phút - Chương 3 - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Đại số 9
-
CHƯƠNG IV. HÀM SỐ y = ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số y = ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số y = ax^2 (a ≠ 0).
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Ôn tập chương IV - Hàm số y = ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
- Đề kiểm tra 15 phút - Chương 4 - Đại số 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 4 - Đại số 9
-
-
PHẦN HÌNH HỌC - TOÁN 9 TẬP 2
-
CHƯƠNG III. GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Ôn tập chương III – Góc với đường tròn
- Đề kiểm tra 15 phút - Chương 3 - Hình học 9
- Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Hình học 9
-
CHƯƠNG IV. HÌNH TRỤ - HÌNH NÓN - HÌNH CẦU
- Bài 1. Hình trụ - Diện tích xung quanh và thể tích hình trụ
- Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Bài 3. Hình cầu. Diện tích hình cầu và thể tích hình cầu
- Ôn tập chương IV – Hình trụ - Hình nón – Hình cầu
- Đề kiểm tra 45 phút (1 tiết) - Chương 4 - Hình học 9
-
BÀI TẬP ÔN CUỐI NĂM - TOÁN 9
-
-
Đề thi học kì 2 mới nhất có lời giải
-
Đề cương ôn tập học kì 2
-
Câu hỏi tự luyện Toán 9
-
Tải 30 đề kiểm tra giữa kì 1 Toán 9
-
Tải 30 đề ôn tập học kì 1 Toán 9
-
Tải 30 đề thi học kì 1 của các trường Toán 9
-
Tải 30 đề kiểm tra giữa kì 2 Toán 9
-
Tải 30 đề ôn tập học kì 2 Toán 9
-
Tải 30 đề thi học kì 2 của các trường Toán 9
Bài 59 trang 90 SGK Toán 9 tập 2
Cho hình bình hành ABCD
Tổng hợp Đề thi vào 10 có đáp án và lời giải
Toán - Văn - Anh
Đề bài
Cho hình bình hành \(ABCD.\) Đường tròn đi qua ba đỉnh \(A, \, B, \, C\) cắt đường thẳng \(CD\) tại \(P\) khác \(C.\) Chứng minh \(AP = AD.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Số đo tổng hai góc đối diện của tứ giác nội tiếp bằng \(180^0.\)
+) Sử dụng tính chất hai đường thẳng song song, tính chất hình bình hành.
Lời giải chi tiết
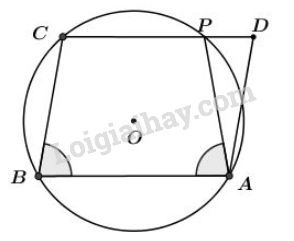
Cách 1:
Do tứ giác \(ABCP\) nội tiếp nên \(\widehat{BAP} + \widehat{BCP} = 180^0.\) (1)
Mà CD // AB nên \(\widehat{ABC}+ \widehat{BCP}= 180^0\) (hai góc trong cùng phía). (2)
Từ (1) và (2) \(\Rightarrow\) \(\widehat{BAP}= \widehat{ABC}.\)
Mà CP // AB (do CD // AB) nên \(ABCP\) là hình thang
Nên \(ABCP\) là hình thang cân (Dấu hiệu nhận biết)
\(\Rightarrow\) \(AP = BC.\) (Tính chất hình thang cân) (3)
Mà \(BC = AD\) (do ABCD là hình bình hành) (4)
Từ (3) và (4) \(\Rightarrow\) \(AP = AD\) (đpcm).
Cách 2:
Vì ABCP là tứ giác nội tiếp nên \(\widehat{ABC}+ \widehat{APC}= 180^0\)
Mà ABCD là hình bình hành nên \(\widehat {ABC} = \widehat {ADC}\) (Tính chất hình bình hành)
Hơn nữa, \(\widehat {APC} + \widehat {APD} = {180^0}\) (2 góc kề bù)
\( \Rightarrow \widehat {APD} = \widehat {ADC}\)
\(\Rightarrow\) Tam giác ADP cân tại A
\(\Rightarrow\) AP = AD (đpcm)
Bình luận
Chia sẻ
- Bài 60 trang 90 SGK Toán 9 tập 2
- Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 3 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 2 - Bài 7 - Chương 3 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 3 - Bài 7 - Chương 3 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 4 - Bài 7 - Chương 3 - Hình học 9
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
