Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 7. Tứ giác nội tiếp

Bài 55 trang 89 SGK Toán 9 tập 2


Cho ABCD là một tứ giác nội tiếp đường tròn tâm M

Đề bài

Cho \(ABCD\) là một tứ giác nội tiếp đường tròn tâm \(M,\) biết \(\widehat {DAB}= 80^0\), \(\widehat {DAM}= 30^0,\)  \(\widehat {BMC}= 70^0\).

Hãy tính số đo các góc \(\widehat {MAB},\)  \(\widehat {BCM},\)  \(\widehat {AMB},\)  \(\widehat {DMC},\)  \(\widehat {AMD},\)  \(\widehat {MCD}\) và \(\widehat {BCD}.\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+ Sử dụng các định lý: “Tổng ba góc trong tam giác bằng \(180^0\)”.

+ Sử dụng tính chất tam giác cân

+ Sử dụng góc ở tâm bằng số đo cung bị chắn.

Lời giải chi tiết

                      

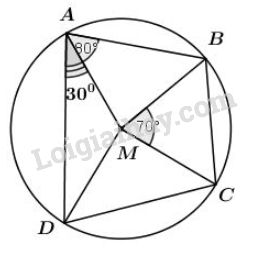
Vì AM nằm giữa AD và AB nên  \(\widehat {MAB}+\widehat {DAM}= \widehat {DAB}\). Do đó, \(\widehat {MAB} = \widehat {DAB} - \widehat {DAM} = {80^0} - {30^0} = {50^0}\) (1)

+)  \(∆MBC\) là tam giác cân  cân tại \(M\) \((MB= MC)\) nên \(\displaystyle \widehat {BCM} = {{{{180}^0} - {{70}^0}} \over 2} = {55^0}\) (2)

+)  \(∆MAB\) là tam giác cân tại \(M\) \((do MA=MB)\) nên \(\widehat {MAB} =\widehat {ABM} = {50^0}\) (theo (1))

Vậy \(\widehat {AMB} = {180^0} - {2.50^0} = {80^0}.\)

Ta có: \(\widehat {BAD}=\dfrac{sđ\overparen{BCD}}{2}\) (số đo góc nội tiếp bằng nửa số đo của cung bị chắn).

\(\Rightarrow sđ\overparen{BCD}=2.\widehat {BAD} = {2.80^0} = {160^0}.\)  

Mà \(sđ\overparen{BC}= \widehat {BMC} = {70^0}\) (số đo góc ở tâm bằng số đo cung bị chắn).

Vậy \(sđ\overparen{DC}={160^0} - {70^0} = {90^0}\) (vì C nằm trên cung nhỏ cung \(BD\)).

\(\Rightarrow\) \(\widehat {DMC} = {90^0}.\)               (4)

Ta có: \(∆MAD\) là tam giác cân cân tại \(M \) \((MA= MD).\) 

\(\Rightarrow\) \(\widehat {AMD} = {180^0} - {2.30^0}=120^0\)   (5)

Có \(∆MCD\) là tam giác vuông cân tại \(M\) \((MC= MD)\) và \(\widehat {DMC} = {90^0}\)

\(\Rightarrow\) \(\widehat {MCD} = \widehat {MDC} = {45^0}.\)  (6)

Theo (2) và (6) và vì CM là tia nằm giữa hai tia \(CB, \, CD\) ta có: \(\widehat {BCD} =\widehat{BCM}+\widehat{MCD} = 55^0+45^0 = {100^0}.\)  


Bình chọn:
4.3 trên 145 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store