 Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
 Bài 2. Hai đường thẳng vuông góc
Bài 2. Hai đường thẳng vuông góc
Bài 5 trang 98 SGK Hình học 11
Cho hình chóp tam giác S.ABC có SA = SB = SC...
Đề bài
Cho hình chóp tam giác \(S.ABC\) có \(SA = SB = SC\) và có \(\widehat{ASB}= \widehat{BSC}=\widehat{CSA}.\) Chứng minh rằng \(SA ⊥ BC, SB ⊥ AC, SC ⊥ AB\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Chứng minh \(\overrightarrow {SA} .\overrightarrow {BC} = 0;\,\,\overrightarrow {SB} .\overrightarrow {AC} = 0;\,\,\overrightarrow {SC} .\overrightarrow {AB} = 0\)
Sử dụng công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \widehat {\left( {\overrightarrow a ;\overrightarrow b } \right)}\)
Lời giải chi tiết
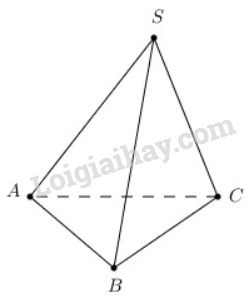
\(\overrightarrow{SA}.\overrightarrow{BC}=\overrightarrow{SA}.(\overrightarrow{SC}-\overrightarrow{SB})\)
\(=\overrightarrow{SA}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SB}\)
\(= SA.SC.\cos\widehat{ASC} - SA.SB.\cos\widehat{ASB} = 0\)
Vậy \(SA ⊥ BC\).
\(\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}.(\overrightarrow{SC}-\overrightarrow{SA})\)
\(=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}\)
\(= SB.SC.\cos\widehat{BSC} - SB.SA.\cos\widehat{ASB} = 0\)
Vậy \(SB ⊥ AC\).
\(\overrightarrow{SC}.\overrightarrow{AB}=\overrightarrow{SC}.(\overrightarrow{SB}-\overrightarrow{SA})\)
\(=\overrightarrow{SC}.\overrightarrow{SB}-\overrightarrow{SC}.\overrightarrow{SA}\)
\(= SC.SB.\cos\widehat{BSC} - SC.SA.\cos\widehat{ASC} = 0\)
Vậy \(SC ⊥ AB\).
Loigiaihay.com
- Bài 6 trang 98 SGK Hình học 11
- Bài 7 trang 98 SGK Hình học 11
- Bài 8 trang 98 SGK Hình học 11
- Bài 4 trang 98 SGK Hình học 11
- Bài 3 trang 97 SGK Hình học 11
>> Xem thêm




















