 Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
 Bài 2. Phương trình lượng giác cơ bản
Bài 2. Phương trình lượng giác cơ bản
Giải bài 5 trang 29 SGK Đại số và Giải tích 11
Giải các phương trình sau:
Video hướng dẫn giải
Giải các phương trình sau:
LG a
\(\begin{array}{l}\tan \left( {x - {{15}^0}} \right) = \frac{{\sqrt 3 }}{3}\\\end{array}\)
Phương pháp giải:
Coi biểu thức sau hàm tan như một ẩn phụ khác, giải tương tự như pt LG cơ bản
\(\begin{array}{l}
\,\,\tan x = \tan a \Leftrightarrow x =a + k180^0 \\ \left( {k \in Z} \right)\\\end{array}\)
Lời giải chi tiết:
Điều kiện \(x - 15^0\neq 90^0+k180^0 \) \(\Leftrightarrow x\neq 105^0+k.180^0.\)
\(tan (x - 15^0) = \frac{\sqrt{3}}{3}\)
\( \Leftrightarrow tan(x-15^0)=tan30^0\)
\(\Leftrightarrow x - 15^0 = 30^0 + k180^0 , (k \in \mathbb{Z}).\)
\(\Leftrightarrow x = 45^0 + k180^0 , (k \in \mathbb{Z}).\) (tm)
Vậy nghiệm của phương trình là: \(x = 45^0 + k180^0 , (k \in \mathbb{Z}).\)
LG b
\(\begin{array}{l}\,\,\cot \left( {3x - 1} \right) = - \sqrt 3 \\\end{array}\)
Phương pháp giải:
Coi biểu thức sau hàm cot như một ẩn phụ lớn, giải tương tự như pt LG cơ bản
\(\begin{array}{l}\,\,\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \,\,\,\left( {k \in Z} \right)\\\end{array}\)
Lời giải chi tiết:
Điều kiện \(3x-1\neq k\pi (k\in \mathbb{Z})\) hay \(x\neq \frac{1+k \pi}{3}(k\in \mathbb{Z})\)
\(\begin{array}{l}
\,\,\,\,\,\,\cot \left( {3x - 1} \right) = - \sqrt 3 \\ \Leftrightarrow \cot \left( {3x - 1} \right) = \cot \left( { - \frac{\pi }{6}} \right)\\
\Leftrightarrow 3x - 1 = - \frac{\pi }{6} + k\pi \\
\Leftrightarrow 3x = 1 - \frac{\pi }{6} + k\pi \\
\Leftrightarrow x = \frac{1}{3} - \frac{\pi }{{18}} + \frac{{k\pi }}{3}\,\,\left( {k \in Z} \right)\,\,\left( {tm} \right)
\end{array}\)
Vậy nghiệm phương trình là \(x=\frac{1}{3}-\frac{\pi }{18}+\frac{k\pi }{3},(k\in \mathbb{Z})\)
LG c
\(\begin{array}{l}\,\,\cos 2x\tan x = 0\\\end{array}\)
Phương pháp giải:
\(\begin{array}{l}\,\,AB = 0 \Leftrightarrow \left[ \begin{array}{l}
A = 0\\
B = 0
\end{array} \right.
\end{array}\)
Lưu ý điều kiện xác định của các hàm tan và cot, hàm phân thức.
Lời giải chi tiết:
Điều kiện \(cosx\neq 0\Leftrightarrow x\neq \frac{\pi }{2}+k\pi (k\in \mathbb{Z})\)
\(\begin{array}{l}
\,\,\,\,\,\,\cos 2x\tan x = 0\\
\Leftrightarrow \left[ \begin{array}{l}
\cos 2x = 0\\
\tan x = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
2x = \frac{\pi }{2} + k\pi \\
x = k\pi
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{4} + \frac{{k\pi }}{2}\\
x = k\pi
\end{array} \right.\,\,\left( {k \in Z} \right)\,\,\,\left( {tm} \right)
\end{array}\)
Vậy nghiệm phương trình là: \(x=\frac{\pi }{4}+\frac{k\pi }{2}(k\in \mathbb{Z})\) hoặc \(x=k\pi (k\in \mathbb{Z})\)
LG d
\(\begin{array}{l}\,\,\sin 3x\cot x = 0
\end{array}\)
Phương pháp giải:
\(\begin{array}{l}\,\,AB = 0 \Leftrightarrow \left[ \begin{array}{l}
A = 0\\
B = 0
\end{array} \right.
\end{array}\)
Lưu ý điều kiện xác định của các hàm tan và cot, hàm phân thức.
Lời giải chi tiết:
ĐK: \(sinx\neq 0\Leftrightarrow x\neq k\pi (k\in \mathbb{Z})\)
\(\begin{array}{l}
\,\,\,\,\,\sin 3x\cot x = 0\\
\Leftrightarrow \left[ \begin{array}{l}
\sin 3x = 0\\
\cot x = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
3x = k\pi \\
x = \frac{\pi }{2} + n\pi
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \frac{{k\pi }}{3}\\
x = \frac{\pi }{2} + n\pi
\end{array} \right.\,\,\,\left( {k,n \in Z} \right)
\end{array}\)
Kết hợp với điều kiện ta thấy khi \(k = 3m,m \in \mathbb{Z}\) thì \(x = \frac{{k\pi }}{3} = \frac{{3m\pi }}{3} = m\pi \,\,\left( {m \in Z} \right)\) \( \Rightarrow \sin x = 0\) không thỏa điều kiện.
Vậy phương trình có nghiệm là: \(x=\frac{k \pi}{3}\) \(\,\left( {k \ne 3m\,\,\left( {m \in Z} \right)} \right)\) và \(x=\frac{\pi }{2}+n\pi \,\,(n \in Z)\).
Chú ý:
Biểu diễn các họ nghiệm trên đường tròn lượng giác để loại nghiệm:
Các nghiệm \(\left[ \begin{array}{l}x = \dfrac{{k\pi }}{3}\\x = \dfrac{\pi }{2} + k\pi \end{array} \right.,k \in \mathbb{Z}\) được biểu diễn bởi các điểm từ A1 đến A8 trên đường tròn lượng giác như hình dưới.
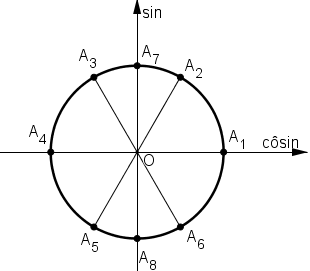
Với điều kiện x ≠ k.π nên các điểm A1 và A4 bị loại.
Vậy họ nghiệm chỉ còn lại các điểm A2; A3; A5; A6; A7; A8 và ta viết được dưới kết quả \(\left[ \begin{array}{l}x = \pm \dfrac{\pi }{3} + k\pi \\x = \dfrac{\pi }{2} + k\pi \end{array} \right.,k \in \mathbb{Z}\).
Loigiaihay.com
- Giải bài 6 trang 29 SGK Đại số và Giải tích 11
- Giải bài 7 trang 29 SGK Đại số và Giải tích 11
- Giải bài 4 trang 29 SGK Đại số và Giải tích 11
- Giải bài 3 trang 28 SGK Đại số và Giải tích 11
- Giải bài 2 trang 28 SGK Đại số và Giải tích 11
>> Xem thêm




















