 Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
 Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Giải bài 5 trang 24 SGK Giải tích 12
Tính giá trị nhỏ nhất của các hàm số sau:
Video hướng dẫn giải
LG a
Tính giá trị nhỏ nhất của các hàm số sau: \(y =|x|\) ;
Phương pháp giải:
- Phá dấu giá trị tuyệt đối đưa hàm số về dạng khoảng.
- Lập bảng biến thiên và kết luận.
Lời giải chi tiết:
\(y=\left| x \right|.\)
Ta có:
\(y = |x| = \left\{ \begin{gathered}
x\text{nếu }x \geqslant 0 \hfill \\
- x\text{ nếu }x < 0 \hfill \\
\end{gathered} \right.\)
Tập xác định: \(D=\mathbb R.\)
\(y' = \left\{ \begin{array}{l}
1\,\text{nếu }\,x > 0\\
- 1\,\text{nếu }\,x < 0
\end{array} \right.\)
Ta có bảng biến thiên:
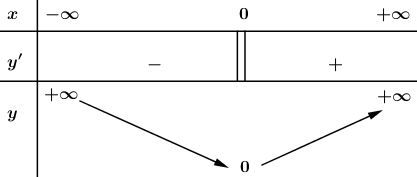
Từ bảng biến thiên ta có hàm số đạt GTNN tại \(x=0;{\min }\,y=0.\)
LG b
\(\displaystyle y =x+{4\over x}\) \(\displaystyle ( x > 0)\).
Phương pháp giải:
- Tìm TXĐ.
- Tính đạo hàm và tìm nghiệm.
- Lập bảng biến thiên rồi kết luận.
Lời giải chi tiết:
\(y=x+\dfrac{4}{x}\ \ \ \left( x>0 \right).\)
Ta có: \(y'=1-\dfrac{4}{{{x}^{2}}}\)
\(\Rightarrow y'=0\Leftrightarrow 1-\dfrac{4}{{{x}^{2}}}=0\)
\(\Leftrightarrow {{x}^{2}}-4=0\Leftrightarrow \left[ \begin{align}& x=-2\notin \left( 0;+\infty \right) \\ & x=2\in \left( 0;+\infty \right) \\ \end{align} \right.\)
Bảng biến thiên:
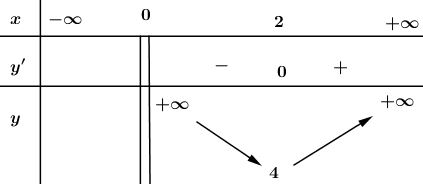
Từ bảng biến thiên ta thấy: \(\underset{\left( 0;+\infty \right)}{\mathop{min}}\,y=4\ \ khi\ \ x=2.\)
Cách khác:
Áp dụng BĐT Cô-si ta có:
\(y = x + \dfrac{4}{x} \ge 2\sqrt {x.\dfrac{4}{x}} = 4 \) \(\Rightarrow y \ge 4 \)
\(\Rightarrow \mathop {\min }\limits_{\left( {0; + \infty } \right)} y = 4\) khi \(x = \dfrac{4}{x} \Leftrightarrow {x^2} = 4 \Leftrightarrow x = 2\).
Loigiaihay.com
- Các dạng toán về giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Giải bài 4 trang 24 SGK Giải tích 12
- Giải bài 3 trang 24 SGK Giải tích 12
- Giải bài 2 trang 24 SGK Giải tích 12
- Giải bài 1 trang 23 SGK Giải tích 12
>> Xem thêm


















