Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - c..
Bài 43 trang 125 SGK Toán 7 tập 1
Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA...
Đề bài
Cho góc \(xOy\) khác góc bẹt. Lấy các điểm \(A,B\) thuộc tia \(Ox\) sao cho \(OA <OB.\)
Lấy các điểm \(C, D\) thuộc tia \(Oy\) sao cho \(OC = OA, OD = OB.\) Gọi \(E\) là giao điểm của \(AD\) và \(BC.\)
Chứng minh rằng:
a) \(AD = BC\);
b) \(∆EAB = ∆ECD\);
c ) \(OE\) là tia phân giác của góc \(xOy.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Nếu hai cạnh và một góc xen giữa của tam giác này bằng hai cạnh và một góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
b) Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
c) Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết
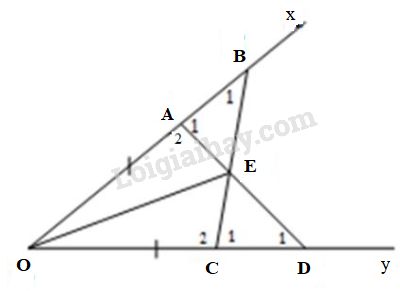
a) Xét \(∆OAD\) và \(∆OCB\) có:
+) \(OA = OC\) (giả thiết)
+) \(\widehat{O}\) chung
+) \(OD = OB\) (giả thiết)
\( \Rightarrow ∆OAD = ∆OCB\) (c.g.c)
\( \Rightarrow AD = BC \) (hai cạnh tương ứng).
b) \(∆OAD = ∆OCB\) (chứng minh câu a)
\( \Rightarrow \widehat{D_1}= \widehat{B_1}\); \(\widehat{A _{2}}= \widehat{ C _{2}}\) (các góc tương ứng)
Mặt khác: \(\widehat {{A_1}} + \widehat {{A_2}} = {180^0}\); \(\widehat {{C_1}} + \widehat {{C_2}} = {180^0}\) (Hai góc kề bù)
Do đó \(\widehat {{A_1}} + \widehat {{A_2}}=\widehat {{C_1}} + \widehat {{C_2}}\)
Mà \(\widehat{A _{2}} = \widehat{ C _{2}}\) nên \(\widehat{A _{1}} = \widehat{ C _{1}}\)
\(AB = OB - OA \) (1)
\(CD = OD - OC \) (2)
\(OA = OC, OB = OD \) (giả thiết) (3)
Từ (1), (2) và (3) suy ra \(AB = CD.\)
Xét \(∆EAB\) và \(∆ECD\) có:
+) \(\widehat{A _{1}} = \widehat{ C _{1}}\) (chứng minh trên)
+) \(AB = CD\) (chứng minh trên)
+) \(\widehat{B_1} = \widehat{D_1}\) (chứng minh trên)
\( \Rightarrow ∆EAB = ∆ECD \) (g.c.g)
c) \(∆EAB = ∆ECD\) (chứng minh câu b)
\( \Rightarrow EA = EC\) (hai cạnh tương ứng).
Xét \(∆OAE\) và \(∆OCE \) có:
+) \(OA=OC\) (giả thiết)
+) \(EA=EC\) (chứng minh trên)
+) \(OE\) cạnh chung
\( \Rightarrow ∆OAE = ∆OCE\) (c .c.c)
\( \Rightarrow \widehat{ AOE} = \widehat{ C OE}\) (hai góc tương ứng)
Vậy \(OE\) là tia phân giác của góc \(xOy.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 44 trang 125 SGK Toán 7 tập 1
- Bài 45 trang 125 SGK Toán 7 tập 1
- Đề kiểm tra 15 phút - Đề số 1 - Bài 2,3,4,5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 2,3,4,5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 2,3,4,5 - Chương 2 - Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
