Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học Bài 1: Đại cương về hàm số

Bài 4 trang 45 SGK Đại số 10 nâng cao


Khảo sát sự biến thiên của mỗi hàm số sau và lập bảng biến thiên của nó:

Lựa chọn câu để xem lời giải nhanh hơn

Khảo sát sự biến thiên của mỗi hàm số sau và lập bảng biến thiên của nó:

LG a

y = x2 + 2x – 2 trên mỗi khoảng \((-∞; -1)\) và \((-1, +∞)\)

Phương pháp giải:

Hàm số f đồng biến trêm K khi và chỉ khi 

\(\forall {x_1},{x_2} \in K\) và \({x_1} \ne {x_2}\) thì \(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} > 0\)

Hàm số f nghịch biến trêm K khi và chỉ khi 

\(\forall {x_1},{x_2} \in K\) và \({x_1} \ne {x_2}\) thì \(\frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} < 0\)

Lời giải chi tiết:

+ Với mọi x1; x2 ∈  \((-∞; -1)\) và x1 ≠ x2 ta có:

f(x2) – f(x1) = x22 + 2x2 – 2 – (x12 + 2x1 – 2)

 = x22 – x12 + 2(x2 – x1) = (x2 – x1)(x1 + x2 + 2)

\(\Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {x_1} + {x_2} + 2\)

Vì x1; x2 ∈  \((-∞; -1)\) nên x1 < -1 và x2 < -1 nên x1 + x2 + 2 < 0

Nên \( \Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} < 0\)

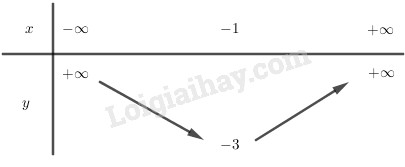
Vậy hàm số y = x2 + 2x – 2 nghịch biến trên \((-∞; -1)\)

+ Với mọi x1; x2 ∈ \((-1, +∞)\) và x1 ≠ x2 ta có:

\({{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {x_1} + {x_2} + 2 > 0\)

(Vì x1; x2 ∈  \((-1;+∞)\) nên x1 > -1; x2 > -1)

Vậy hàm số y =  x2 + 2x – 2 đồng biến trên \((-1, +∞)\)

Bảng biến thiên:

LG b

\(y = -2x^2 + 4x + 1 \) trên mỗi khoảng \((-∞; 1)\) và \((1, +∞)\)

Lời giải chi tiết:

+ Với mọi x1; x2 ∈ \((-∞; 1)\) và x1 ≠ x2 ta có:

f(x2) – f(x1) = (-2x22 + 4x2 + 1) – (-2x12 + 4x1 + 1)

= -2(x22 - x12) + 4(x2 - x1)

\(=  - 2\left( {{x_2} - {x_1}} \right)\left( {{x_2} + {x_1}} \right) + 4\left( {{x_2} - {x_1}} \right)\)

\(= 2\left( {{x_2} - {x_1}} \right)\left( { - {x_2} - {x_1} + 2} \right)\)

\( = {\rm{ }}2\left( {{x_2} - {x_1}} \right)\left[ {2 - \left( {{x_1} + {x_2}} \right)} \right]\)

\( \Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} \) \(=2\left[ {2 - \left( {{x_1} + {x_2}} \right)} \right]\)

Vì x1 < 1 và x2 < 1 nên \({x_1} + {x_2} < 2 \Rightarrow 2 - \left( {{x_1} + {x_2}} \right) > 0\)

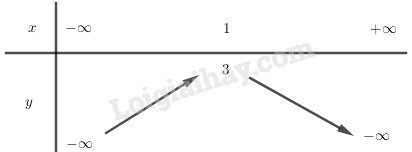
Vậy hàm số \(y = -2x^2+ 4x + 1\) đồng biến trên khoảng \((-∞; 1)\)

+ Với mọi x1; x2 ∈ \((1; +∞)\) thì x1 > 1 và x2 > 1 và x1 ≠ x2 ta có:

\({x_1} + {x_2} > 2 \Rightarrow 2 - \left( {{x_1} + {x_2}} \right) < 0\)

Do đó \({{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} \)\(=2\left[ {2 - \left( {{x_1} + {x_2}} \right)} \right]\) < 0

Vậy hàm số \(y = -2x^2 + 4x + 1\) nghịch biến trên khoảng \((1; +∞)\)

Bảng biến thiên:

LG c

\(y = {2 \over {x - 3}}\) trên mỗi khoảng \((-∞; 3)\) và \((3, +∞)\)

Lời giải chi tiết:

+ Với x1, x2 ∈ \((- ∞; 3)\) với x1 ≠ x2 ta có:

\(\eqalign{
& f({x_2}) - f({x_1}) = {2 \over {{x_2} - 3}} - {2 \over {{x_1} - 3}} \cr 
& = {{2({x_1} - 3) - 2({x_2} - 3)} \over {({x_1} - 3)({x_2} - 3)}} \cr&= {{2({x_1} - {x_2})} \over {({x_1} - 3)({x_2} - 3)}} \cr 
& \Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {{ - 2} \over {({x_1} - 3)({x_2} - 3)}} \cr} \)

(vì x1 < 3; x2 < 3 nên (x1 – 3)(x2 – 3) > 0)

\(\Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}}<0\)

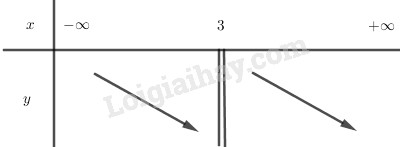
Vậy hàm số \(y = {2 \over {x - 3}}\)  nghịch biến trên \((- ∞; 3)\)

+ Với x1, x2 ∈ \((3; +∞)\) với x1 ≠ x2 ta có:

\({{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {{ - 2} \over {({x_1} - 3)({x_2} - 3)}} < 0\)

(vì x1 > 3; x2 > 3 nên (x1 – 3)(x2 – 3) > 0)

Vậy hàm số \(y = {2 \over {x - 3}}\) nghịch biến trên \((3; + ∞)\)

Bảng biến thiên:

Loigiaihay.com


Bình chọn:
4.3 trên 21 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

2k8 Tham gia ngay group chia sẻ, trao đổi tài liệu học tập miễn phí

>> Học trực tuyến Lớp 10 tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua