Bài 4 trang 12 SGK Hình học 10
Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành
Đề bài
Cho tam giác \(ABC\). Bên ngoài tam giác vẽ các hình bình hành \(ABIJ, BCPQ, CARS\). Chứng minh rằng \(\overrightarrow{RJ} + \overrightarrow{IQ} + \overrightarrow{PS}= \overrightarrow{0}.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Với quy tắc ba điểm tùy ý \(A, \, \, B, \, \, C\) ta luôn có:
\(+ )\;\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (quy tắc ba điểm).
\( + )\;\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \) (quy tắc trừ).
Lời giải chi tiết
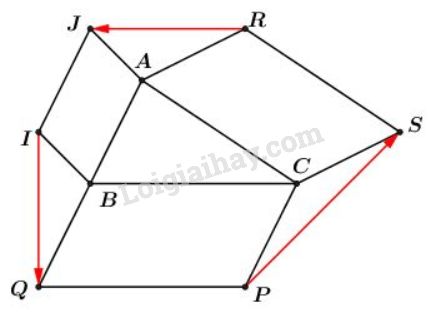
Ta xét tổng:
\((\overrightarrow{RJ} +\overrightarrow{IQ} +\overrightarrow{PS})+ ( \overrightarrow{JI}+ \overrightarrow{QP}+\overrightarrow{SR}) \)
\(=\overrightarrow{RJ} +\overrightarrow{IQ} +\overrightarrow{PS}+ \overrightarrow{JI}+ \overrightarrow{QP}+\overrightarrow{SR}\)
\(\begin{array}{l}
= \left( {\overrightarrow {RJ} + \overrightarrow {JI} } \right) + \left( {\overrightarrow {IQ} + \overrightarrow {QP} } \right) + \left( {\overrightarrow {PS} + \overrightarrow {SR} } \right)\\
= \overrightarrow {RI} + \overrightarrow {IP} + \overrightarrow {PR} \\
= \overrightarrow {RP} + \overrightarrow {PR}
\end{array}\)
\(= \overrightarrow{RR}= \overrightarrow{0}\)(1)
Mặt khác, ta có \(ABIJ, BCPQ\) và \(CARS\) là các hình bình hành nên:
\(\overrightarrow{JI} = \overrightarrow{AB}\)
\(\overrightarrow{QP} = \overrightarrow{BC}\)
\(\overrightarrow{SR}= \overrightarrow{CA}\)
\(\Rightarrow \overrightarrow{JI}+\overrightarrow{QP}+\overrightarrow{SR}\)\(= \overrightarrow{AB}+ \overrightarrow{BC}+\overrightarrow{CA}= \overrightarrow{AA}= \overrightarrow{0}\) (2)
Từ (1) và (2) suy ra :
\(\overrightarrow{RJ} + \overrightarrow{IQ} + \overrightarrow{PS}\)\(= \overrightarrow{0}.\) (đpcm)
Cách khác:
Ta có:
AJIB là hình bình hành nên \(\overrightarrow {AJ} = \overrightarrow {BI} \)
\( \Rightarrow \overrightarrow {AJ} + \overrightarrow {IB} = \overrightarrow {BI} + \overrightarrow {IB} = \overrightarrow {BB} = \overrightarrow 0 \)
Tương tự như vậy:
BCPQ là hình bình hành nên \(\overrightarrow {BQ} + \overrightarrow {PC} = \overrightarrow 0 \)
CARS là hình bình hành nên \(\overrightarrow {CS} + \overrightarrow {RA} = \overrightarrow 0 \)
Do đó:
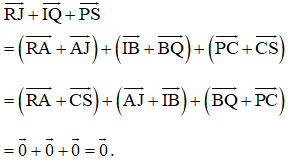
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 5 trang 12 SGK Hình học 10
- Bài 6 trang 12 SGK Hình học 10
- Bài 7 trang 12 SGK Hình học 10
- Bài 8 trang 12 SGK Hình học 10
- Bài 9 trang 12 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Ph/hs Tham Gia Nhóm Để Cập Nhật Điểm Thi, Điểm Chuẩn Miễn Phí
