Bài 4 trang 104 SGK Đại số và Giải tích 11
Tìm cấp số nhân có sau số hạng, biết rằng tổng của năm số hạng đầu là 31 và tổng của năm số hạng sau là 62.
Đề bài
Tìm cấp số nhân có sáu số hạng, biết rằng tổng của năm số hạng đầu là \(31\) và tổng của năm số hạng sau là \(62\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng công thức số hạng tổng quát của CSN: \({u_n} = {u_1}{q^{n - 1}}\) và công thức tổng n số hạng đầu tiên của CSN: \({S_n} = \dfrac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\).
Lời giải chi tiết
Giả sử có cấp số nhân: \({u_1},{u_2},{u_3},{u_4},{u_5},{u_6}\)
Theo giả thiết ta có:
\({u_1} + {u_2} + {u_3} + {u_4} + {u_5} = 31\). (1)
\({u_2} + {u_3} + {u_4} + {u_5} + {u_6} = 62\). (2)
Nhân hai vế của (1) với \(q\), ta được: \({u_1}q + {u_2}q + {u_3}q + {u_4}q + {u_5}q = 31q\)
\( \Leftrightarrow \)\({u_2} + {u_3} + {u_4} + {u_5} + {u_6} = 31q\) (3)
Từ (2) và (3) \(\Rightarrow 62 = 31.q \Rightarrow q = 2\).
Ta có \({S_5} = 31 \Leftrightarrow \dfrac{{{u_1}\left( {1 - {2^5}} \right)}}{{1 - 2}} = 31\) \( \Leftrightarrow 31{u_1} = 31 \Leftrightarrow {u_1} = 1\)
Vậy ta có cấp số nhân là: \(1, 2, 4, 8, 16, 32\).
Cách khác:
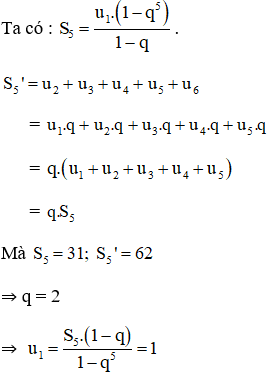
Vậy ta có cấp số nhân là: \(1, 2, 4, 8, 16, 32\).
Loigiaihay.com
- Bài 5 trang 104 SGK Đại số và Giải tích 11
- Bài 6 trang 104 SGK Đại số và Giải tích 11
- Bài 3 trang 103 SGK Đại số và Giải tích 11
- Bài 2 trang 103 SGK Đại số và Giải tích 11
- Bài 1 trang 103 SGK Đại số và Giải tích 11
>> Xem thêm




















