Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - c..
Bài 37 trang 123 SGK Toán 7 tập 1
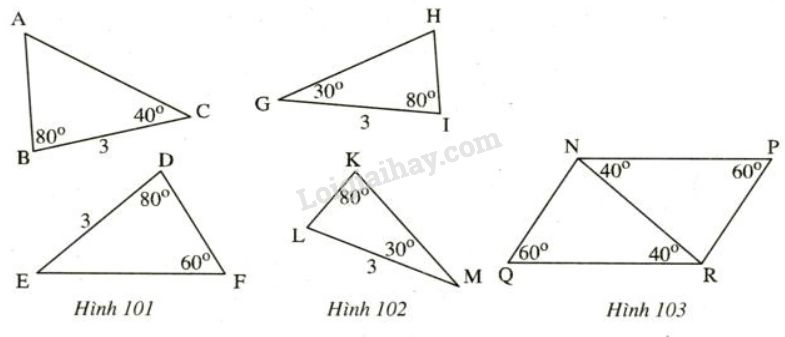
Trên mỗi hình 101,102,103 có tam giác nào bằng nhau? Vì sao?
Đề bài
Trên mỗi hình 101, 102, 103 có tam giác nào bằng nhau? Vì sao?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết
*Hình 101: \(\widehat E = {180^0} - \widehat D - \widehat F \\ = {180^0} - {80^0} - {60^0} = {40^0}\)
- Xét \(∆ABC\) và \(∆FDE\) (Hình 101)
+) \(\widehat{B} = \widehat{D}=80^o\)
+) \(BC=DE=3\)
+) \(\widehat{C}=\widehat{E}=40^o\)
\( \Rightarrow ∆ABC=∆FDE\) (g.c.g)
*Hình 102: \(\widehat L = {180^0} - \widehat K - \widehat M \\= {180^0} - {80^0} - {30^0} = {70^0}\)
- Xét \(\Delta HIG\) và \(\Delta LKM\) (Hình 102)
+ ) \(\widehat G = \widehat M \)
+ ) \(\widehat I = \widehat K \)
+ ) \(GI = ML\) .Tuy nhiên, \(\widehat G,\; \widehat I \) cùng kề với cạnh \(GI\), còn \(\widehat M \) và \( \widehat K\) không cùng kề với cạnh \(ML\) nên \(\Delta HIG\) không bằng \(\Delta LKM\).
* Hình 103: \(\widehat {QNR} = {180^0} - \widehat {NRQ} - \widehat {RQN} \\= {180^0} - {40^0} - {60^0} = {80^0}\\
\widehat {NRP} = {180^0} - \widehat {RPN} - \widehat {PNR}\\ = {180^0} - {60^0} - {40^0} = {80^0}\)
- Xét \(∆NQR\) và \(∆RPN\) (Hình 103)
+) \(\widehat{QNR}=\widehat{NRP}=80^0\)
+) \(NR\) là cạnh chung.
+) \(\widehat{NRQ}=\widehat{RNP}=40^0\)
Suy ra \(∆NQR=∆RPN\) (g.c.g)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 38 trang 124 SGK Toán 7 tập 1
- Bài 39 trang 124 SGK Toán 7 tập 1
- Bài 40 trang 124 SGK Toán 7 tập 1
- Bài 41 trang 124 SGK Toán 7 tập 1
- Bài 42 trang 124 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
