Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - c..
Bài 34 trang 123 SGK Toán 7 tập 1
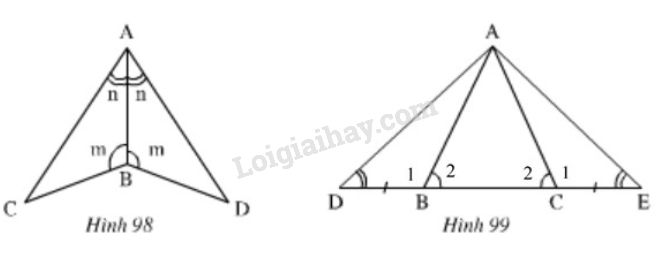
Trên mỗi hình 98,99 có tam giác nào bằng nhau? Vì sao?
Đề bài
Trên mỗi hình 98,99 có tam giác nào bằng nhau? Vì sao?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết
Xem hình 98)
Xét \(∆ABC\) và \(∆ABD\) có:
+) \(\widehat{CAB}=\widehat{DAB}\) (giả thiết)
+) \(AB\) là cạnh chung.
+) \(\widehat{ABC}=\widehat{ABD}\) (giả thiết)
\( \Rightarrow ∆ABC=∆ABD\) (g.c.g)
Xem hình 99) (gọi tên như hình vẽ)
Ta có:
\(\widehat{B_{1}}+\widehat{B_{2}}=180^0\) (hai góc kề bù).
\(\widehat{C _{1}}+ \widehat{C _{2}}=180^0\) (hai góc kề bù)
Mà \(\widehat{B_{2}}=\widehat{C _{2}}\) (giả thiết) nên \(\widehat{B_{1}}=\widehat{C _{1}}\)
* Xét \(∆ABD\) và \(∆ACE\) có:
+) \(\widehat{B_{1}}=\widehat{C _{1}}\) (chứng minh trên)
+) \(BD=EC\) (giả thiết)
+) \(\widehat{D } = \widehat{E }\) (giả thiết)
\( \Rightarrow ∆ABD=∆ACE\) (g.c.g)
Cách 1: Ta có:
\(DC=DB+BC\)
\(EB=EC+CB\)
Mà \(DB=EC\)
Do đó: \(DC=EB\)
* Xét \(∆ADC\) và \(∆AEB\) có:
+) \(\widehat{D }=\widehat{E }\) (giả thiết)
+) \(\widehat{C _{2}}=\widehat{B_{2}}\) (giả thiết)
+) \(DC=EB\) (chứng minh trên)
\(\Rightarrow ∆ADC=∆AEB\) (g.c.g)
Cách 2: Vì ∆ABD=∆ACE nên AD=AE; AB=AC( 2 cạnh tương ứng)
Do đó: ∆ADC=∆AEB (c-c-c)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 35 trang 123 SGK Toán 7 tập 1
- Bài 36 trang 123 SGK Toán 7 tập 1
- Bài 37 trang 123 SGK Toán 7 tập 1
- Bài 38 trang 124 SGK Toán 7 tập 1
- Bài 39 trang 124 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
