Giải bài 3 trang 61 SGK Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số:
Video hướng dẫn giải
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số:
LG a
a) \(y=x^{4\over3}\) ;
Phương pháp giải:
Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Tính y', tìm các điểm mà tại đó có y' bằng 0 hoặc không xác định, xét dấu y' và suy ra các chiều biến thiên của hàm số. Tìm các cực trị, các giới hạn tại vô cực và các đường tiệm cận để lập BBT của đồ thị hàm số.
Bước 3: Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị hàm số.
Lời giải chi tiết:
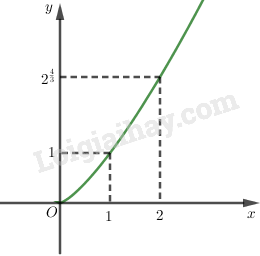
Hàm số \(y=x^{4\over3}\)
*) Tập xác định: \(D=(0;+\infty )\).
+) Sự biến thiên:
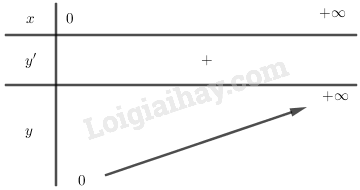
Ta có: \(y' = \displaystyle{4 \over 3}.{x^{{1 \over 3}}}>0,\forall x>0 \)
- Hàm số đồng biến trên khoảng \((0;+\infty)\)
- Giới hạn đặc biệt: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \).
- Đồ thị hàm số không có tiệm cận.
- Bảng biến thiên
*) Đồ thị: Đồ thị hàm số qua \((1;1)\), \((2;\root 3 \of {{2^4}} )\).
LG b
b) \(y=x^{-3}\).
Lời giải chi tiết:
Hàm số \(y = {x^{ - 3}}\)
*) Tập xác định: \(D=\mathbb ℝ \backslash {\rm{\{ }}0\} \).
*) Sự biến thiên:
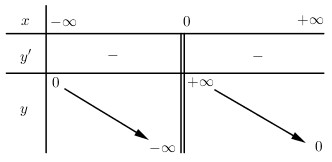
Ta có: \(y' = - 3{x^{ - 4}} < 0,\forall x \in D\)
- Hàm nghịch biến trong khoảng \((-∞;0)\) và \((0; +∞)\).
- Giới hạn đặc biệt:
\(\eqalign{
& \mathop {\lim }\limits_{x \to {0^ + }} y = + \infty \cr
& \mathop {\lim }\limits_{x \to {0^ - }} y = - \infty \cr
& \mathop {\lim }\limits_{x \to \pm \infty } y = 0 \cr }\)
- Đồ thị hàm số nhận trục tung làm tiệm cận đứng, trục hoành làm tiệm cận ngang.
- Bảng biến thiên
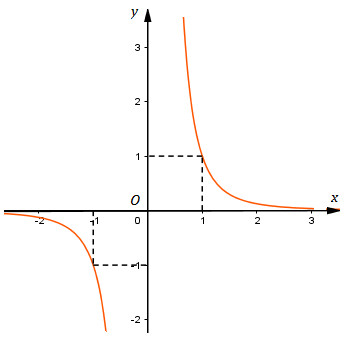
*) Đồ thị:
Đồ thị qua \((-1;-1)\), \((1;1)\), \(\left( {2;\dfrac{1}{8}} \right)\), \(\left( {-2;\dfrac{-1}{8}} \right)\).
Hàm số đã cho là hàm số lẻ nên đồ thị có tâm đối xứng là gốc tọa độ.
Loigiaihay.com
- Giải bài 4 trang 61 SGK Giải tích 12
- Giải bài 5 trang 61 SGK Giải tích 12
- Các công thức lãi kép
- Giải bài 2 trang 61 SGK Giải tích 12
- Giải bài 1 trang 60 SGK Giải tích 12
>> Xem thêm