Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 4. Đường trung bình của tam giác, của hình thang

Bài 28 trang 80 SGK Toán 8 tập 1


Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thằng EF cắt BD ở I, cắt AC ở K.

Đề bài

Cho hình thang \(ABCD\) (\(AB // CD\)), \(E\) là trung điểm của \(AD,\) \(F\) là trung điểm của \(BC.\) Đường thẳng \(EF\) cắt \(BD\) ở \(I,\) cắt \(AC\) ở \(K.\)

a) Chứng minh rằng \(AK = KC, BI = ID.\)

b) Cho \(AB = 6\,cm, CD = 10\,cm.\) Tính các độ dài \(EI, KF, IK.\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Áp dụng:

- Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

- Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên.

- Đường trung bình của hình thang thì song song với hai cạnh đáy.

- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

- Định lí: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.

Lời giải chi tiết

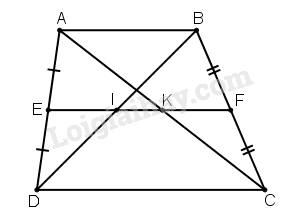
a) Hình thang \(ABCD\) có \(E, F\) lần lượt là trung điểm của \(AD\) và \(BC\) (giả thiết)

\( \Rightarrow  EF\) là đường trung bình của hình thang \(ABCD\) (dấu hiệu nhận biết đường trung bình của hình thang )

\( \Rightarrow EF // AB // CD\) (tính chất đường trung bình của hình thang) 

\( \Rightarrow FK//AB, EI//AB\)

Xét \(∆ABC\) có: \(F\) là trung điểm của \(BC\) (giả thiết) và \(FK // AB\) (chứng minh trên)

\( \Rightarrow  AK = KC\) (Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba )

Xét \(∆ABD\) có: \(E\) là trung điểm của \(AD\) (giả thiết) và \(EI // AB\) (chứng minh trên)

\( \Rightarrow  DI = IB\) (Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba ).        

b) Vì \(EF\) là đường trung bình của hình thang \(ABCD\) (chứng minh trên)

nên \(EF = \dfrac{AB+CD}{2} = \dfrac{6+10}{2} = 8\,cm\) (tính chất đường trung bình của hình thang)

Xét \(∆ABD\) có: \(AE = ED\) (giả thiết) và \(DI = IB\) (chứng minh trên)

 \( \Rightarrow  EI\) là đường trung bình của \(∆ABD\) (dấu hiệu nhận biết đường trung bình của  tam giác)

 \( \Rightarrow  EI = \dfrac{1}{2}.AB = \dfrac{1}{2}.6 = 3\; (cm)\) (tính chất đường trung bình của  tam giác)

Xét \(∆ABC\) có: \(BF = FC\) (giả thiết) và \(AK = KC\) (chứng minh trên)

 \( \Rightarrow  KF\) là đường trung bình của \( ∆ABC\) (dấu hiệu nhận biết đường trung bình của  tam giác)

 \( \Rightarrow  KF = \dfrac{1}{2}.AB = \dfrac{1}{2}.6 = 3\; (cm)\) (tính chất đường trung bình của  tam giác)

Lại có \(EF = EI + IK + KF\)

nên \(IK = EF - (EI + KF) = 8 - (3 + 3)\)\(\, = 2 \;(cm).\)

Loigiaihay.com


Bình chọn:
4.6 trên 388 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store