Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 4. Đường thẳng song song và đường thẳng cắt nhau

Bài 25 trang 55 SGK Toán 9 tập 1


Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:

Đề bài

a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ: 

\(y = \dfrac{2}{3}x + 2\);                                       \(y =  - \dfrac{3}{2}x + 2\)

b) Một đường thẳng song song với trục hoành \(Ox\), cắt trục tung \(Oy\) tại điểm có tung độ bằng \(1\), cắt các đường thẳng \(y = \dfrac{2}{3}x + 2\) và \(y =  - \dfrac{3}{2}x + 2\) theo thứ tự tại hai điểm \(M\) và \(N\). Tìm tọa độ của hai điểm \(M\) và \(N\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Cách vẽ đồ thị hàm số \(y=ax+b,\ (a \ne 0)\): Đồ thị hàm số \(y=ax+b \, \, (a\neq 0)\) là đường thẳng:

+) Cắt trục hoành tại điểm \(A(-\dfrac{b}{a}; \, 0).\) 

+) Cắt trục tung tại điểm \(B(0;b).\) 

Xác định tọa độ hai điểm \(A\) và \(B\) sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số  \(y=ax+b \, \, (a\neq 0).\)

b) +) Đường thẳng song song với trục \(Ox\) có dạng \(y=a\), đường thẳng song song với trục \(Oy\) có dạng \(x=b\).

+) Hai đường thẳng \(y=ax+b,\ y=a'x+b'\) cắt nhau tại \(A\). Hoành độ điểm \(A\) là nghiệm của phương trình: \(ax+b=a'x+b\). Giải phương trình tìm \(x\). Thay \(x\) tìm được vào công thức hàm số trên tìm được tung độ điểm \(A\).

Lời giải chi tiết

a) Hàm số \(y = \dfrac{2}{3}x + 2\)

Cho \(x= 0 \Rightarrow y = \dfrac{2}{3}. 0+ 2=0+2=2 \Rightarrow A(0; 2)\)

Cho \(y= 0 \Rightarrow 0 = \dfrac{2}{3}. x+ 2 \Rightarrow x=-3 \Rightarrow B(-3; 0)\)

Đường thẳng đi qua hai điểm \(A,\ B\) là đồ thị của hàm số \(y = \dfrac{2}{3}x + 2\).

+) Hàm số \(y =- \dfrac{3}{2}x + 2\) 

Cho \(x= 0 \Rightarrow y = -\dfrac{3}{2}. 0+ 2=0+2=2 \Rightarrow A(0; 2)\)

Cho \(y=0 \Rightarrow y = -\dfrac{3}{2}. x+ 2 \Rightarrow x= \dfrac{4}{3}  \Rightarrow C {\left(\dfrac{4}{3}; 0 \right)}\)

Đường thẳng đi qua hai điểm \(A,\ C\) là đồ thị của hàm số \(y = -\dfrac{3}{2}x + 2\).

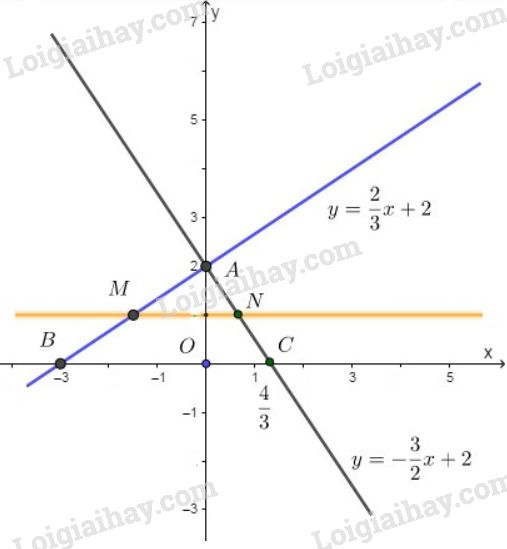
b) Đường thẳng song song với trục \(Ox\) cắt trục \(Oy\) tại điểm có tung độ \(1\) có dạng: \(y=1\).

Vì \(M\) là giao của đường thẳng \(y=\dfrac{2}{3}x+2\) và \(y=1\) nên hoành độ của \(M\) là nghiệm của phương trình: 

\(\dfrac{2}{3}x+2=1\)

\(\Leftrightarrow \dfrac{2}{3}x=1-2\)

\(\Leftrightarrow \dfrac{2}{3}x=-1\)

\(\Leftrightarrow x=-\dfrac{3}{2}\)

Do đó tọa độ \(M\) là: \(M{\left( -\dfrac{3}{2}; 1 \right)}\).

Vì \(N\) là giao của đường thẳng \(y=-\dfrac{3}{2}x+2\) và \(y=1\) nên hoành độ của \(N\) là nghiệm của phương trình:

\(-\dfrac{3}{2}x+2=1\)

\(\Leftrightarrow -\dfrac{3}{2}x=1-2\)

\(\Leftrightarrow -\dfrac{3}{2}x=-1\)

\(\Leftrightarrow x=\dfrac{2}{3}\)

Do đó tọa độ \(N\) là: \(N{\left( \dfrac{2}{3}; 1 \right)}\).

Loigiaihay.com


Bình chọn:
4.5 trên 102 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store