 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Bài 1. Giá trị lượng giác của một góc bất kỳ từ 0 độ đế..
Bài 1. Giá trị lượng giác của một góc bất kỳ từ 0 độ đế..
Bài 2 trang 40 SGK Hình học 10
Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK.
Đề bài
Cho \(AOB\) là tam giác cân tại \(O\) có \(OA = a\) và có các đường cao \(OH\) và \(AK.\) Giả sử \(\widehat {AOH} = \alpha. \) Tính \(AK\) và \(OK\) theo \(a\) và \(α.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Sử dụng công thức lượng giác đối với góc nhọn ta có: \(sin \alpha =\frac{cạnh \, \, đối}{cạnh \, \, huyền} \) và \(cos \alpha =\frac{cạnh \, \, kề}{cạnh \, \, huyền}\)
Lời giải chi tiết
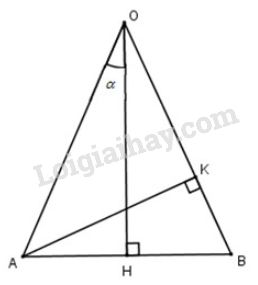
TH1: \(\alpha < 45^0\)
Do tam giác \(OAB\) cân tại \(O\) nên ta có \(\widehat {AOB} = 2\widehat {AOH}=2\alpha < 90^0 \)
Tam giác \(OKA\) vuông tại \(K\) nên ta có:
\(\sin \widehat {AOK} = \frac{{AK}}{{OA}} \)
\(\Rightarrow AK = OA.\sin \widehat {AOK} \)\(\Rightarrow AK = a.\sin 2\alpha. \)
\(\cos \widehat {AOK} = \frac{{OK}}{{OA}} \)
\(\Rightarrow OK = OA.cos\widehat {AOK} \)\(\Rightarrow OK = a.\cos 2\alpha .\)
TH2: \(\alpha > 45^0\)
Do tam giác \(OAB\) cân tại \(O\) nên ta có \(\widehat {AOB} = 2\widehat {AOH}=2\alpha > 90^0 \)
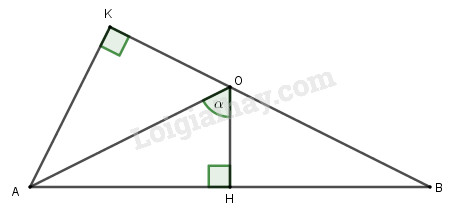
Tam giác AKO vuông tại K có AO=a, \(\widehat {AOK} = {180^0} - \widehat {AOB} = {180^0} - 2\alpha \)
Khi đó:
\(\begin{array}{l}\sin \widehat {AOK} = \frac{{AK}}{{OA}}\\ \Rightarrow AK = OA\sin \widehat {AOK}\\ = a\sin \left( {{{180}^0} - 2\alpha } \right) = a\sin 2\alpha \\\cos \widehat {AOK} = \frac{{OK}}{{OA}}\\ \Rightarrow OK = OA\cos \widehat {AOK}\\ = a\cos \left( {{{180}^0} - 2\alpha } \right) = - a\cos 2\alpha \end{array}\)
Loigiaihay.com
- Bài 3 trang 40 SGK Hình học 10
- Bài 4 trang 40 SGK Hình học 10
- Bài 5 trang 40 SGK Hình học 10
- Bài 6 trang 40 SGK Hình học 10
- Bài 1 trang 40 SGK Hình học 10
>> Xem thêm



















