Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 3. Hình thang cân

Bài 16 trang 75 SGK Toán 8 tập 1


Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Đề bài

Cho tam giác \(ABC\) cân tại \(A\), các đường phân giác \(BD, CE\) (\(D ∈ AC, E ∈ AB\)). Chứng minh rằng \(BEDC\) là hình thang cân có đáy nhỏ bằng cạnh bên.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Hai tam giác bằng nhau có các cạnh tương ứng bằng nhau.

- Tam giác cân có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau.

- Hai đường thẳng song song khi có cặp góc đồng vị bằng nhau. 

- Hình thang là tứ giác có hai cạnh đối song song.

- Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.

Lời giải chi tiết

 

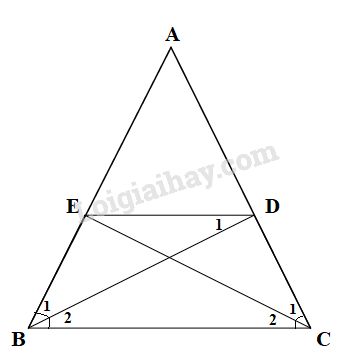
\(\Delta ABC\) cân tại \(A\) (giả thiết)

\( \Rightarrow \left\{ \begin{array}{l}
AB = AC\\
\widehat {ABC} = \widehat {ACB}
\end{array} \right.\)  (tính chất tam giác cân)

Vì \(BD, CE\) lần lượt là phân giác của \(\widehat {ABC}\) và \(\widehat {ACB}\) (giả thiết) 

\( \Rightarrow \left\{ \begin{array}{l}
\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{{\widehat {ABC}}}{2}\\
\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{{\widehat {ACB}}}{2}
\end{array} \right.\) (tính chất tia phân giác)

Mà \(\widehat {ABC} = \widehat {ACB}\) (chứng minh trên)

\( \Rightarrow \widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)

 Xét \(∆ABD\) và  \(∆ACE\) có:

+) \(AB = AC\) (chứng minh trên)

+) \(\widehat{A}\) chung

+) \(\widehat {{B_1}} = \widehat {{C_1}}\) (chứng minh trên)

\( \Rightarrow \Delta ABD = \Delta ACE{\rm{ }}\left( {g.c.g} \right) \)

\(\Rightarrow A{\rm{D}} = A{\rm{E}}\) (\(2\) cạnh tương ứng).

Ta có \(AD =  AE\) (chứng minh trên) nên  \(∆ADE\) cân tại \(A\) (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow \widehat {A{\rm{ED}}} = \widehat {AD{\rm{E}}}\) (tính chất tam giác cân)

Xét \(∆ADE\) có:  \(\widehat {A{\rm{ED}}} + \widehat {AD{\rm{E}}} + \widehat A = {180^0}\) (định lý tổng ba góc trong tam giác)

\(\begin{array}{l}
\Rightarrow 2\widehat {A{\rm{ED}}} + \widehat A = {180^0}\\
\Rightarrow \widehat {A{\rm{ED}}} = \dfrac{{{{180}^0} - \widehat A}}{2}\left( 1 \right)
\end{array}\)

Xét \(∆ABC\) có: \(\widehat A +\widehat {ABC} + \widehat {ACB} = {180^0}\) (định lý tổng ba góc trong tam giác)

Mà \(\widehat {ABC} = \widehat {ACB}\) (chứng minh trên)

\(\begin{array}{l}
\Rightarrow \widehat {2ABC} + \widehat A = {180^0}\\
\Rightarrow \widehat {ABC}= \dfrac{{{{180}^0} - \widehat A}}{2}\left( 2 \right)
\end{array}\)

Từ (1) và (2) \(\Rightarrow \widehat{A{\rm{ED}}}\) = \(\widehat{ABC}\), mà hai góc này là hai góc đồng vị nên suy ra \(DE // BC\) (dấu hiệu nhận biết hai đường thẳng song song)

Do đó \(BEDC\) là hình thang (dấu hiệu nhận biết hình thang).

Lại có \(\widehat{ABC}\) = \(\widehat{ACB}\)  (chứng minh trên)

Nên \(BEDC\) là hình thang cân (dấu hiệu nhận biết hình thang cân)

Ta có:

\(DE//BC \Rightarrow \widehat {{D_1}} = \widehat {{B_2}}\) (so le trong)

Lại có \(\widehat{B_{2}}\) = \(\widehat{B_{1}}\) (chứng minh trên) nên \(\widehat{B_{1}}\) = \(\widehat{{D_{1}}}\)

\( \Rightarrow \Delta EB{\rm{D}}\) cân tại \(E\) (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow EB = E{\rm{D}}\) (tính chất tam giác cân).

Vậy \(BEDC\) là hình thang cân có đáy nhỏ bằng cạnh bên.

Loigiaihay.com


Bình chọn:
4.4 trên 589 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua