 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Bài 12 trang 106 SGK Toán 9 tập 1
Gọi I là điểm thuộc dây AB sao cho AI=1cm. Kẻ dây CD đi qua I và vuông góc với AB.
Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD
Đề bài
Cho đường tròn tâm \(O\) bán kính \(5cm\), dây \(AB\) bằng \(8cm\).
a) Tính khoảng cách từ tâm \(O\) đến dây \(AB\).
b) Gọi \(I\) là điểm thuộc dây \(AB\) sao cho \(AI=1cm\). Kẻ dây \(CD\) đi qua \(I\) và vuông góc với \(AB\). Chứng minh rằng \(CD=AB\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) +) Sử dụng định lý: Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Sử dụng định lí Pytago: \(\Delta{ABC}\), vuông tại \(A\) thì \(BC^2=AC^2+AB^2\).
b) Sử dụng định lý: Trong một đường tròn, hai dây cách đều nhau thì bằng nhau.
Lời giải chi tiết
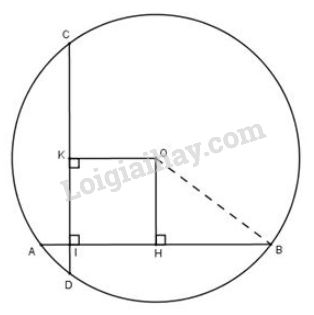
a) Kẻ \(OH\perp AB\) tại H
Khi đó, đường tròn (O) có OH là 1 phần đường kính vuông góc với dây AB tại H
Suy ra \(H\) là trung điểm của dây \(AB\) (Theo định lí 2 - trang 103)
\(\Rightarrow HA=HB=\dfrac{AB}{2}=\dfrac{8}{2}=4cm.\)
Xét tam giác \(HOB\) vuông tại \(H\), theo định lí Pytago, ta có:
\(OB^2=OH^2+HB^2 \Leftrightarrow OH^{2}=OB^{2}-HB^{2}\)
\(\Leftrightarrow OH^2=5^{2}-4^{2}=25-16=9\Rightarrow OH=3(cm)\).
Vậy khoảng cách từ tâm \(O\) đến dây \(AB\) là \(3cm\).
b) Vẽ \(OK\perp CD\) tại K
Tứ giác \(KOHI\) có ba góc vuông \((\widehat K=\widehat H=\widehat I=90^0)\) nên là hình chữ nhật, suy ra \(OK=HI\).
Ta có \(HI=AH-AI=4-1=3cm\), suy ra \(OK=3cm.\)
Vậy \(OH=OK = 3cm.\)
Hai dây \(AB\) và \(CD\) cách đều tâm nên chúng bằng nhau.
Do đó \(AB = CD.\)
Loigiaihay.com
- Bài 13 trang 106 SGK Toán 9 tập 1
- Bài 14 trang 106 SGK Toán 9 tập 1
- Bài 15 trang 106 SGK Toán 9 tập 1
- Bài 16 trang 106 SGK Toán 9 tập 1
- Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 2 - Hình học 9
>> Xem thêm
Các bài khác cùng chuyên mục



















