Bài 11 trang 72 SGK Toán 9 tập 2
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A và B
Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD
Đề bài
Cho hai đường tròn bằng nhau \((O)\) và \((O')\) cắt nhau tại hai điểm \(A\) và \(B\). Kẻ các đường kính \(AOC, AO'D\). Gọi \(E\) là giao điểm thứ hai của \(AC\) với đường tròn \((O')\).
a) So sánh các cung nhỏ \(\overparen{BC}, \overparen{BD}\).
b) Chứng minh rằng \(B\) là điểm chính giữa của cung \(\overparen{EBD}\) ( tức điểm \(B\) chia cung \(\overparen{EBD}\) thành hai cung bằng nhau: \(\overparen{BE}\) = \(\overparen{BD}\) ).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
* Chứng minh hai tam giác bằng nhau hoặc tam giác cân để suy ra hai dây bằng nhau.
Từ đó sử dụng định lý: Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+) Hai cung bằng nhau căng hai dây bằng nhau.
+) Hai dây bằng nhau căng hai cung bằng nhau.
Lời giải chi tiết
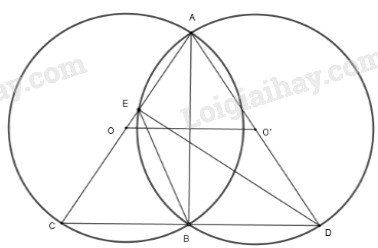
a) Vì \(\left( O \right)\) và \(\left( {O'} \right)\) cắt nhau tại hai điểm \(A\) và \(B\) nên \(OO' \bot AB\) (định lý)
Xét tam giác \(ADC\) có \(OO'\) là đường trung bình (vì \(O\) là trung điểm \(AC,O'\) là trung điểm \(AD\)) nên \(OO'//CD\) , suy ra \(AB \bot CD\) (quan hệ từ vuông góc đến song song).
Xét tam giác \(ADC\) có \(AC = AD\) (vì hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) có cùng bán kính) nên \(\Delta ACD\) cân tại \(A\) có \(AB\) là đường cao nên \(AB\) cũng là đường trung tuyến, suy ra \(BC = BD\) hay \(\overparen{BC}\) =\(\overparen{BD}\) (vì \(\left( O \right)\) và \(\left( {O'} \right)\) là hai đường tròn bằng nhau).
b) Vì \(A,E,D\) cùng thuộc đường tròn (O') nên O'E = O'A=O'D = \(\frac{1}{2}AD\) nên tam giác \(AED\) vuông tại \(E\) (Đường trung tuyến ứng với 1 cạnh bằng nửa cạnh đó thì tam giác đó vuông)
\(\Rightarrow \widehat {AED} \widehat {DEC} = 90^\circ .\)
Xét tam giác \(DEC\) vuông tại \(E\) có \(B\) là trung điểm của CD (cmt)\(\Rightarrow EB = \dfrac{{DC}}{2} = BD = EB\) (Đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra \(\overparen{EB}\)=\(\overparen{BD}\) (2 dây bằng nhau chắn 2 cung bằng nhau), do đó \(B\) là điểm chính giữa cung \(ED.\).
- Bài 12 trang 72 SGK Toán 9 tập 2
- Bài 13 trang 72 SGK Toán 9 tập 2
- Bài 14 trang 72 SGK Toán 9 tập 2
- Đề kiểm tra 15 phút - Đề số 1 - Bái 2 - Chương 3 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 3 - Hình học 9
>> Xem thêm
Các bài khác cùng chuyên mục




















