 Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
 Bài 6. Khái niệm về phép dời hình và hai hình bằng nhau
Bài 6. Khái niệm về phép dời hình và hai hình bằng nhau
Bài 1 trang 23 SGK Hình học 11
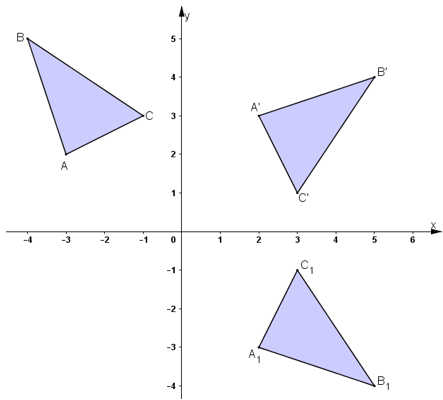
Trong mặt phẳng Oxy cho các điểm A(-3;2), B(-4;5) và C(-1;3)
Video hướng dẫn giải
Trong mặt phẳng \(Oxy\) cho các điểm \(A(-3;2), B(-4;5)\) và \(C(-1;3)\)
LG a
Chứng minh rằng các điểm \(A'(2;3), B'(5;4)\) và \(C'(3;1)\) theo thứ tự là ảnh của \(A, B\) và \(C\) qua phép quay tâm \(O\) góc \( -90^{\circ}\)
Phương pháp giải:
Sử dụng định nghĩa phép quay
\({Q_{\left( {O;\alpha } \right)}}\left( M \right) = M' \) \(\Leftrightarrow \left\{ \begin{array}{l}
OM' = OM\\
\left( {OM,OM'} \right) = \alpha
\end{array} \right.\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}
\overrightarrow {OA} = \left( { - 3;2} \right);\;\overrightarrow {OA'} = \left( {2;3} \right).\\
OA = \sqrt {{{( - 3)}^2} + {2^2}} = \sqrt {{2^2} + {3^2}} = OA'\\
\overrightarrow {OA} \,.\,\overrightarrow {OA'} = \left( { - 3} \right).2 + 2.3 = 0\\
\Rightarrow \widehat {AOA'} = {90^o}\\
\Rightarrow \left( {OA;\;OA'} \right) = - \widehat {AOA'} = - {90^o}\\
\Rightarrow A' = {Q_{\left( {O; - {{90}^o}} \right)}}(A).
\end{array}\)
Tương tự ta cũng có \({Q_{\left( {O; - {{90}^0}} \right)}}\left( B \right) = B',\) \({Q_{\left( {O; - {{90}^0}} \right)}}\left( C \right) = C'\).
Chú ý:
Cách giải tham khảo (công thức mở rộng)
Sử dụng biểu thức tọa độ của phép quay: Ảnh của điểm \(M(x;y)\) qua phép quay tâm \(O\) góc quay \(\alpha\) là điểm \(M'(x';y')\) với \(x';y'\) thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
(hình bên)
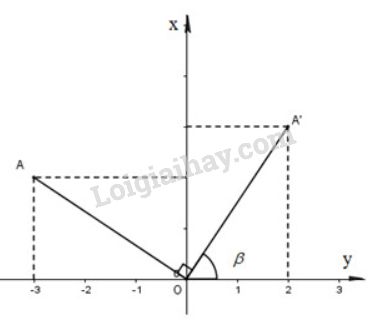
Phép quay tâm góc \(-90^0\) biến điểm \(M(x;y)\) thành điểm \(M'(x';y')\) với \(\left\{ \begin{array}{l}x' = x\cos \left( { - {{90}^0}} \right) - y\sin \left( { - {{90}^0}} \right) = y\\y' = x\sin \left( { - {{90}^0}} \right) + y\cos \left( { - {{90}^0}} \right) = - x\end{array} \right.\)
\( \Rightarrow A'\left( {2;3} \right);\,\,B'\left( {5;4} \right);\,\,C'\left( {3;1} \right)\) lần lượt là ảnh của \(A, B, C\) qua phép quay tâm \(O,\) góc quay \(-90^0\).
LG b
Gọi tam giác \({A_{1}}\)\({B_{1}}\)\({C_{1}}\) là ảnh của tam giác \(ABC\) qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm \(O\) góc \( -90^{\circ}\) và phép đối xứng qua trục \(Ox\). Tìm tọa độ các đỉnh của tam giác \({A_{1}}^{}\)\({B_{1}}^{}\)\({C_{1}}^{}\)
Phương pháp giải:
Thực hiện liên tiếp phép quay tâm \(O\) góc quay \(-90^0\) và phép đối xứng trục \(Ox\) trên mặt phẳng tọa độ \(Oxy.\)
Lời giải chi tiết:
(Hình 1.26)
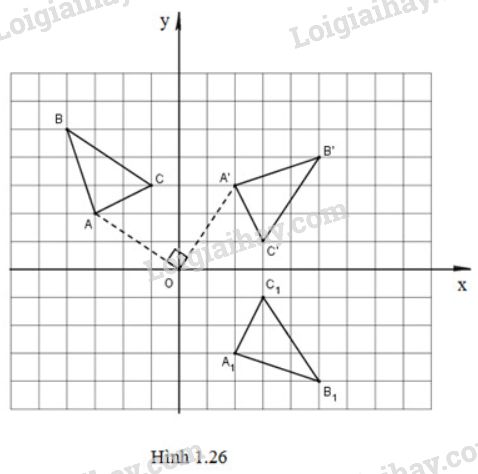
Gọi tam giác \({A_{1}}^{}\)\({B_{1}}^{}\)\({C_{1}}^{}\) là ảnh của tam giác \(A'B'C'\) qua phép đối xứng trục \(Ox\).
Khi đó,
\(\begin{array}{l}
{A_1} = {D_{Ox}}\left( {A'} \right) \Rightarrow {A_1}\left( {2; - 3} \right)\\
{B_1} = {D_{Ox}}\left( {B'} \right) \Rightarrow {B_1}\left( {5; - 4} \right)\\
{C_1} = {D_{Ox}}\left( {C'} \right) \Rightarrow {C_1}\left( {3; - 1} \right)
\end{array}\)
Vậy \({A_{1}}(2;-3), {B_{1}}^{}(5;-4), {C_{1}}^{}(3;-1).\)
Loigiaihay.com
- Bài 2 trang 24 SGK Hình học 11
- Bài 3 trang 24 SGK Hình học 11
- Câu hỏi 5 trang 23 SGK Hình học 11
- Câu hỏi 4 trang 22 SGK Hình học 11
- Câu hỏi 3 trang 21 SGK Hình học 11
>> Xem thêm



















