Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học ÔN TẬP CUỐI NĂM - ĐẠI SỐ VÀ GIẢI TÍCH 11

Bài 1 trang 178 SGK Đại số và Giải tích 11


Chứng minh rằng: cos 2(x + k π) = cos 2x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos2x.

Video hướng dẫn giải

Lựa chọn câu để xem lời giải nhanh hơn

Cho hàm số \(y = \cos 2x\)

LG a

Chứng minh rằng: \(\cos 2(x + k π) = \cos 2x\) với mọi số nguyên \(k\). Từ đó vẽ đồ thị (C) của hàm số \(y = \cos2x\).

Phương pháp giải:

Sử dụng chu kì tuần hoàn của hàm số cos

Lời giải chi tiết:

Ta có: \(\cos 2(x + k π) = \cos (2x + k2 π) = \cos 2x\).

_ Từ kết quả trên ta suy ra hàm số \(y = \cos 2x\) là hàm số tuần hoàn có chu kì là \(π\).

_ Do đó, ta chỉ cần vẽ đồ thị hàm số  \(y = \cos 2x\) trên \([0, π]\) và tịnh tiến nó song song với  trục \(Ox\) các đoạn có độ dài là \(π\).

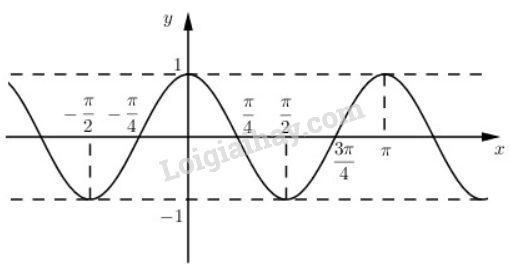
Bảng giá trị đặc biệt

\(x\)

\(0\)

  \({\pi  \over 4}\)  \({\pi  \over 2}\)

            \({{3\pi } \over 4}\)

\(π\)

\(\cos 2x\)

\(1\)

\(0\)

\(-1\)

\(0\)

\(1\)

Đồ thị hàm số :

LG b

Viết phương trình tiếp tuyến của đồ thị (C)  tại điểm có hoành độ \(x = {\pi  \over 3}\)

Phương pháp giải:

Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x=x_0\) là: \(y - {y_0} = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\)

Lời giải chi tiết:

Ta có: \({x_0} = {\pi  \over 3} \Rightarrow {y_0} = \cos {{2\pi } \over 3} =  - {1 \over 2}\)

Ta lại có:

\(\eqalign{
& f'(x) = - 2\sin 2x \cr 
& \Rightarrow f'({\pi \over 3}) = - 2\sin {{2\pi } \over 3} = - \sqrt 3 \cr} \)

 Vậy phương trình tiếp tuyến cần tìm là:

\(y + {1 \over 2} =  - \sqrt 3 (x - {\pi  \over 3}) \Leftrightarrow y =  - \sqrt 3 x + {{\pi \sqrt 3 } \over 3} - {1 \over 2}\)

LG c

Tìm tập xác định của hàm số \(z = \sqrt {{{1 - \cos 2x} \over {1 + {{\cos }^2}2x}}} \)

Phương pháp giải:

Hàm số \(y = \sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0\), sử dụng tính chất \(\cos \alpha  \in \left[ { - 1;1} \right]\).

Lời giải chi tiết:

Ta có:

\(|cos 2x| ≤ 1\) nên \(1 – cos 2x ≥ 0 ,∀ x ∈ \mathbb R\).

\( \Rightarrow \dfrac{{1 - \cos 2x}}{{1 + {{\cos }^2}2x}} \ge 0\,\,\forall x \in R\)

Do đó, tập xác định của hàm số \(z\) là \(\mathbb R\).

Loigiaihay.com


Bình chọn:
3.7 trên 9 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua